题目内容
11.关于x的不等式组$\left\{\begin{array}{l}{x-a≤0}\\{2x+3a>0}\end{array}\right.$的解集中至少有5个整数解,则正数a的最小值是( )| A. | 3 | B. | 2 | C. | 1 | D. | $\frac{2}{3}$ |
分析 首先解不等式组求得不等式组的解集,然后根据不等式组的整数解的个数从而确定a的范围,进而求得最小值.
解答 解:$\left\{\begin{array}{l}{x-a≤0①}\\{2x+3a>0②}\end{array}\right.$,
解①得x≤a,
解②得x>-$\frac{3}{2}$a.
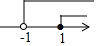
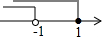
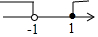
则不等式组的解集是-$\frac{3}{2}$a<x≤a.
∵不等式至少有5个整数解,则a的范围是a≥2.
a的最小值是2.
故选B.
点评 本题考查一元一次不等式组的整数解,确定a的范围是本题的关键.

练习册系列答案
相关题目
2.计算:(-$\frac{1}{2}$)2-1=( )
| A. | -$\frac{5}{4}$ | B. | -$\frac{1}{4}$ | C. | -$\frac{3}{4}$ | D. | 0 |
19.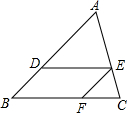 如图,在△ABC中,DE∥BC,∠ADE=∠EFC,AD:BD=5:3,CF=6,则DE的长为( )
如图,在△ABC中,DE∥BC,∠ADE=∠EFC,AD:BD=5:3,CF=6,则DE的长为( )
 如图,在△ABC中,DE∥BC,∠ADE=∠EFC,AD:BD=5:3,CF=6,则DE的长为( )
如图,在△ABC中,DE∥BC,∠ADE=∠EFC,AD:BD=5:3,CF=6,则DE的长为( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
6.多边形的外角和等于( )
| A. | 180° | B. | 360° | C. | 720° | D. | (n-2)•180° |