题目内容
在正方形ABCD中,点E在BC边所在直线上,过E作EF⊥AC于F,G为线段AE的中点,连接BF、FG、G B。
B。
证明:△BGF是等腰直角三角形。
(1)如图1,若点E在BC边上,
∵EF⊥AC于点F,∴∠AFE=90°。
∵在Rt△AEF中,G为斜边AE的中点,∴ 。
。
在Rt△ABE中,同理可得 。
。
∴GF=GB。∴△BGF为等腰三角形。
又∵AG= BG,AG=FG,∴∠BGE=2∠BAG,∠EGF=2∠GAF。
BG,AG=FG,∴∠BGE=2∠BAG,∠EGF=2∠GAF。
又∵∠BAC=45°,∴∠BGF=∠BGE ∠EGF=2(∠BAG
∠EGF=2(∠BAG ∠GAF)=2∠BAC=
∠GAF)=2∠BAC= 90°。
90°。
∴△BGF为等腰直角三角形。

(3)如图3,若点E在CB的延长线上,
同(1)可证△BGF为
 等腰三角形,
等腰三角形,
∵AG=BG,AG=FG,∴∠BGE=2∠BAG,∠EGF=2∠GAF。
又∵∠BAC=45°,∴∠BGF=∠EGF  ∠BGE =2(∠GAF
∠BGE =2(∠GAF  ∠BAG)=2∠BAC=90°。
∠BAG)=2∠BAC=90°。
∴△BGF为等腰直角三角形。
综 上所述,△BGF是等腰直角三角形。
上所述,△BGF是等腰直角三角形。

【考点】等腰直角三角形的判定,正方形的性质,直角三角形斜边上中线的性质,三角形外角性质。
【分析】分点E在BC边上,在BC的延长线上,点E在CB的延长线上三种情况证明即可。

练习册系列答案
相关题目

 ,的整数解仅有
,的整数解仅有 1,2,那么适合这个不等式组的整数a,b组成的有序数对[a,b
1,2,那么适合这个不等式组的整数a,b组成的有序数对[a,b ]共有 个。
]共有 个。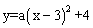 与y轴的交点,点B是这条抛物线上的另一点,且AB∥x轴,则以AB为斜边的等腰直角三角形ABC的顶点C的坐标为 .
与y轴的交点,点B是这条抛物线上的另一点,且AB∥x轴,则以AB为斜边的等腰直角三角形ABC的顶点C的坐标为 .
 销售量-成本-投资)。
销售量-成本-投资)。 式(不必写出自变量x的取值范围),并求出x为何值时,y的
式(不必写出自变量x的取值范围),并求出x为何值时,y的 值最大?
值最大? 中,
中, ,
, ,则由“
,则由“ ”可以判定( )
”可以判定( )

 B.
B.
 D.以上答案都不对
D.以上答案都不对 C.3组 D.4组
C.3组 D.4组  且BD⊥DC,AB=AD=DC=4,则
且BD⊥DC,AB=AD=DC=4,则 =【 】
=【 】
 B
B .
. C.
C.
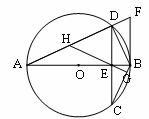

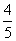
 ,DF=9,求⊙O的半径。
,DF=9,求⊙O的半径。 沿x轴方向平移m个单位后,与直线
沿x轴方向平移m个单位后,与直线 的交点在第一象限,则m的取值范围是【 】
的交点在第一象限,则m的取值范围是【 】 B.
B. C.
C. D.
D.