题目内容
如图,AB为⊙O的直径,弦CD与AB相交于E,DE=EC,过点B的切线与AD的延长线交于F,过E作EG⊥BC于G,延长GE交AD于H.
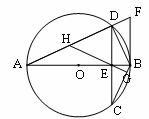

(1)求证:AH=HD;
(2)若AE:AD=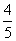
 ,DF=9,求⊙O的半径。
,DF=9,求⊙O的半径。
(1)证明见解析;(2)10.
【解析】

∴AB⊥CD,
∴∠C+∠CBE=90°,
∵EG⊥BC ,
,
∴∠C+∠CEG=90°,
∴∠CBE=∠CEG,
∵∠CBE= ∠CDA,∠CEG=∠DEH,
∠CDA,∠CEG=∠DEH,
∴∠CDA=∠DEH,
∴HD =EH,
=EH,
∵∠A+∠ADC=90°,∠AEH+∠DEH=90°,
∴AH=EH,
∴AH=HD;

∴AB=
 ,
,
∴⊙O的半径为10.
考点:1.切线的 性质
性质 ;2.垂径定理;3.圆周角定理;4.相似三角形的判定与性质.
;2.垂径定理;3.圆周角定理;4.相似三角形的判定与性质.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
 的交点的个数为【 】
的交点的个数为【 】 B。
B。
 B.10cm C.9cm D
B.10cm C.9cm D .8cm
.8cm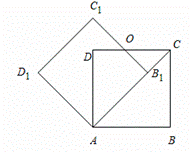


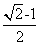
 C.
C.
 D.
D.

 的长。
的长。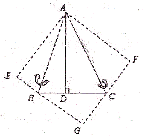

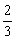 ),且与y轴交于点C(0,
),且与y轴交于点C(0,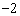 ),与x轴交于A,B两点(点A在点B的左边)。
),与x轴交于A,B两点(点A在点B的左边)。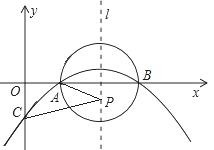
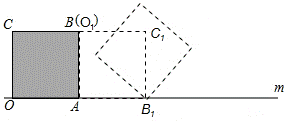

 中,
中,

 .将
.将 绕点
绕点 按顺时针方向旋转n度后得到
按顺时针方向旋转n度后得到 ,此时点
,此时点 在
在 边上,斜边
边上,斜边 交
交 边于点
边于点
 ,则n的大小和图中阴影部分的面积分别为【 】
,则n的大小和图中阴影部分的面积分别为【 】
 B.
B. C.
C. D.
D.