题目内容
2. 如图,若AD=CD=BD,∠A=26°,则∠BCD=64°.
如图,若AD=CD=BD,∠A=26°,则∠BCD=64°.
分析 根据等腰三角形的性质得到∠ACD=∠A=26°,由三角形的外角的性质得到∠BDC=2∠A=52°,于是得到结论.
解答 解:∵AD=CD=BD,∠A=26°,
∴∠ACD=∠A=26°,
∴∠BDC=2∠A=52°,
∴∠BCD=$\frac{180°-∠BDC}{2}$=64°.
故答案为:64°.
点评 本题考查了等腰三角形的性质,三角形的内角和外角的性质,熟练掌握等腰三角形的性质是解题的关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
13.如图,甲、乙、丙三个三角形中和△ABC全等的图形是( )


| A. | 甲和乙 | B. | 乙和丙 | C. | 只有乙 | D. | 只有丙 |
10.用一个平面去截一个圆锥,截面图形不可能是( )
| A. |  | B. |  | C. |  | D. |  |
12.某水库大坝的横断面是梯形,坝内斜坡的坡度i=1:$\sqrt{3}$,坝外斜坡的坡度i=1:1,则两个坡角的和为( )
| A. | 75° | B. | 105° | C. | 90° | D. | 60° |
 如图,在△ABC中,∠ACB=90°,CD⊥AB,D为垂足,AC=6cm,BC=8cm.
如图,在△ABC中,∠ACB=90°,CD⊥AB,D为垂足,AC=6cm,BC=8cm.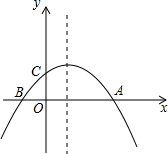 如图,已知抛物线y=-$\frac{1}{a}$(x+2)(x-a)(a>0)与x轴交于点A,B(点A在点B右侧),与y轴交于点C,抛物线过点N(6,一4).
如图,已知抛物线y=-$\frac{1}{a}$(x+2)(x-a)(a>0)与x轴交于点A,B(点A在点B右侧),与y轴交于点C,抛物线过点N(6,一4).