题目内容
 (2012•临沂)如图,正方形ABCD的边长为4cm,动点P、Q同时从点A出发,以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动,设运动时间为x(单位:s),四边形PBDQ的面积为y(单位:cm2),则y与x(0≤x≤8)之间函数关系可以用图象表示为( )
(2012•临沂)如图,正方形ABCD的边长为4cm,动点P、Q同时从点A出发,以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动,设运动时间为x(单位:s),四边形PBDQ的面积为y(单位:cm2),则y与x(0≤x≤8)之间函数关系可以用图象表示为( )分析:根据题意结合图形,分①0≤x≤4时,根据四边形PBDQ的面积=△ABD的面积-△APQ的面积,列出函数关系式,从而得到函数图象,②4≤x≤8时,根据四边形PBDQ的面积=△BCD的面积-△CPQ的面积,列出函数关系式,从而得到函数图象,再结合四个选项即可得解.
解答:解:①0≤x≤4时,
∵正方形的边长为4cm,
∴y=S△ABD-S△APQ,
=
×4×4-
•x•x,
=-
x2+8,
②4≤x≤8时,
y=S△BCD-S△CPQ,
=
×4×4-
•(8-x)•(8-x),
=-
(8-x)2+8,
所以,y与x之间的函数关系可以用两段二次函数图象表示,纵观各选项,只有B选项图象符合.
故选B.
∵正方形的边长为4cm,
∴y=S△ABD-S△APQ,
=
| 1 |
| 2 |
| 1 |
| 2 |
=-
| 1 |
| 2 |
②4≤x≤8时,
y=S△BCD-S△CPQ,
=
| 1 |
| 2 |
| 1 |
| 2 |
=-
| 1 |
| 2 |
所以,y与x之间的函数关系可以用两段二次函数图象表示,纵观各选项,只有B选项图象符合.
故选B.
点评:本题考查了动点问题的函数图象,根据题意,分别求出两个时间段的函数关系式是解题的关键.

练习册系列答案
相关题目
 (2012•临沂)如图,AB∥CD,DB⊥BC,∠1=40°,则∠2的度数是( )
(2012•临沂)如图,AB∥CD,DB⊥BC,∠1=40°,则∠2的度数是( ) (2012•临沂)如图是一个几何体的三视图,则这个几何体的侧面积是( )
(2012•临沂)如图是一个几何体的三视图,则这个几何体的侧面积是( )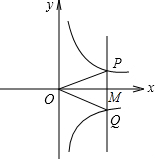 (2012•临沂)如图,若点M是x轴正半轴上任意一点,过点M作PQ∥y轴,分别交函数y=
(2012•临沂)如图,若点M是x轴正半轴上任意一点,过点M作PQ∥y轴,分别交函数y= (2012•临沂)如图,AB是⊙O的直径,点E为BC的中点,AB=4,∠BED=120°,则图中阴影部分的面积之和为( )
(2012•临沂)如图,AB是⊙O的直径,点E为BC的中点,AB=4,∠BED=120°,则图中阴影部分的面积之和为( )