题目内容
(2012•临沂)如图,点A在x轴上,OA=4,将线段OA绕点O顺时针旋转120°至OB的位置.
(1)求点B的坐标;
(2)求经过点A、O、B的抛物线的解析式;
(3)在此抛物线的对称轴上,是否存在点P,使得以点P、O、B为顶点的三角形是等腰三角形?若存在,求点P的坐标;若不存在,说明理由.
(1)求点B的坐标;

(2)求经过点A、O、B的抛物线的解析式;
(3)在此抛物线的对称轴上,是否存在点P,使得以点P、O、B为顶点的三角形是等腰三角形?若存在,求点P的坐标;若不存在,说明理由.
分析:(1)首先根据OA的旋转条件确定B点位置,然后过B做x轴的垂线,通过构建直角三角形和OB的长(即OA长)确定B点的坐标.
(2)已知O、A、B三点坐标,利用待定系数法求出抛物线的解析式.
(3)根据(2)的抛物线解析式,可得到抛物线的对称轴,然后先设出P点的坐标,而O、B坐标已知,可先表示出△OPB三边的边长表达式,然后分①OP=OB、②OP=BP、③OB=BP三种情况分类讨论,然后分辨是否存在符合条件的P点.
(2)已知O、A、B三点坐标,利用待定系数法求出抛物线的解析式.
(3)根据(2)的抛物线解析式,可得到抛物线的对称轴,然后先设出P点的坐标,而O、B坐标已知,可先表示出△OPB三边的边长表达式,然后分①OP=OB、②OP=BP、③OB=BP三种情况分类讨论,然后分辨是否存在符合条件的P点.
解答:解:(1)如图,过B点作BC⊥x轴,垂足为C,则∠BCO=90°,
∵∠AOB=120°,
∴∠BOC=60°,
又∵OA=OB=4,
∴OC=
OB=
×4=2,BC=OB•sin60°=4×
=2
,
∴点B的坐标为(-2,-2
);

(2)∵抛物线过原点O和点A、B,
∴可设抛物线解析式为y=ax2+bx,
将A(4,0),B(-2.-2
)代入,得
,
解得
,
∴此抛物线的解析式为y=-
x2+
x
(3)存在,
如图,抛物线的对称轴是直线x=2,直线x=2与x轴的交点为D,设点P的坐标为(2,y),
①若OB=OP,
则22+|y|2=42,
解得y=±2
,
当y=2
时,在Rt△POD中,∠PDO=90°,sin∠POD=
=
,
∴∠POD=60°,
∴∠POB=∠POD+∠AOB=60°+120°=180°,
即P、O、B三点在同一直线上,
∴y=2
不符合题意,舍去,
∴点P的坐标为(2,-2
)
②若OB=PB,则42+|y+2
|2=42,
解得y=-2
,
故点P的坐标为(2,-2
),
③若OP=BP,则22+|y|2=42+|y+2
|2,
解得y=-2
,
故点P的坐标为(2,-2
),
综上所述,符合条件的点P只有一个,其坐标为(2,-2
),
∵∠AOB=120°,
∴∠BOC=60°,
又∵OA=OB=4,
∴OC=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∴点B的坐标为(-2,-2
| 3 |

(2)∵抛物线过原点O和点A、B,
∴可设抛物线解析式为y=ax2+bx,
将A(4,0),B(-2.-2
| 3 |
|
解得
|
∴此抛物线的解析式为y=-
| ||
| 6 |
2
| ||
| 3 |
(3)存在,
如图,抛物线的对称轴是直线x=2,直线x=2与x轴的交点为D,设点P的坐标为(2,y),
①若OB=OP,
则22+|y|2=42,
解得y=±2
| 3 |
当y=2
| 3 |
| PD |
| OP |
| ||
| 2 |
∴∠POD=60°,
∴∠POB=∠POD+∠AOB=60°+120°=180°,
即P、O、B三点在同一直线上,
∴y=2
| 3 |
∴点P的坐标为(2,-2
| 3 |
②若OB=PB,则42+|y+2
| 3 |
解得y=-2
| 3 |
故点P的坐标为(2,-2
| 3 |
③若OP=BP,则22+|y|2=42+|y+2
| 3 |
解得y=-2
| 3 |
故点P的坐标为(2,-2
| 3 |
综上所述,符合条件的点P只有一个,其坐标为(2,-2
| 3 |
点评:此题融合了函数解析式的确定、等腰三角形的判定等知识,综合程度较高,但属于二次函数综合题型中的常见考查形式,没有经过分类讨论而造成漏解是此类题目中易错的地方.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2012•临沂)如图,AB∥CD,DB⊥BC,∠1=40°,则∠2的度数是( )
(2012•临沂)如图,AB∥CD,DB⊥BC,∠1=40°,则∠2的度数是( ) (2012•临沂)如图是一个几何体的三视图,则这个几何体的侧面积是( )
(2012•临沂)如图是一个几何体的三视图,则这个几何体的侧面积是( )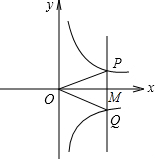 (2012•临沂)如图,若点M是x轴正半轴上任意一点,过点M作PQ∥y轴,分别交函数y=
(2012•临沂)如图,若点M是x轴正半轴上任意一点,过点M作PQ∥y轴,分别交函数y= (2012•临沂)如图,AB是⊙O的直径,点E为BC的中点,AB=4,∠BED=120°,则图中阴影部分的面积之和为( )
(2012•临沂)如图,AB是⊙O的直径,点E为BC的中点,AB=4,∠BED=120°,则图中阴影部分的面积之和为( )