题目内容
18.抛物线y=-2(x-3)2+1的开口向向下,顶点坐标是(3,1),对称轴是x=-1,函数的最最大值是1.分析 已知抛物线解析式为顶点式,可根据顶点式求抛物线的开口方向,对称轴、顶点坐标以及函数的最值.
解答 解:∵y=-2(x-3)2+1,二次项系数为-2<0,
∴抛物线开口向下,对称轴为直线x=-1,顶点坐标为(3,1),函数有值,为1.
故答案为:向下,(3,1),x=-1,最大,1.
点评 本题考查了二次函数解析式的顶点式与其性质的联系,根据二次项系数的符号确定开口方向,得到最值,根据顶点式确定顶点坐标及对称轴.

练习册系列答案
相关题目
9.下列说法正确的是( )
| A. | 三角形的内心到三角形三个顶点的距离相等 | |
| B. | 三点确定一个圆 | |
| C. | 平分弦的直径垂直于弦 | |
| D. | 相等的弧所对的圆心角相等 |
3. 已知x2=5,那么在数轴上与实数x对应的点可能是( )
已知x2=5,那么在数轴上与实数x对应的点可能是( )
 已知x2=5,那么在数轴上与实数x对应的点可能是( )
已知x2=5,那么在数轴上与实数x对应的点可能是( )| A. | P2 | B. | P2或P4 | C. | P1或P5 | D. | P1或P3 |
10.关于抛物线y=-$\frac{1}{2}$(x+2)2+1,下列说法正确的是( )
| A. | 当x=2时,y有最小值1 | B. | 当x=-2时,y有最大值1 | ||
| C. | 当x=2时,y有最大值1 | D. | 当x=-2时,y有最小值1 |
7.下列各组单项式中,为同类项的是( )
| A. | a3与a2 | B. | a2与a | C. | 2xy与2x | D. | -3与7 |
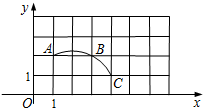 如图,在平面直角坐标系中,过格点A、B、C作一圆弧.
如图,在平面直角坐标系中,过格点A、B、C作一圆弧.