题目内容

若抛物线y=x2+2x+a的顶点在x轴的下方，则a的取值范围是
 
．
考点：抛物线与x轴的交点
专题：
分析：根据抛物线y=x2+2x+a的开口向上，顶点在x轴的下方，可以得到与x轴有两个交点，即方程x2+2x+a=0有两个不相等的实数根，由此可以求出a的取值范围．
解答：解：∵抛物线y=x2+2x+a的开口向上，顶点在x轴的下方，
而与x轴有两个交点，
方程x2+2x+a=0有两个不相等的实数根，
即b2-4ac=4-4a＞0，
∴a＜1．
故答案是：a＜1．
点评：本题考查了抛物线与x轴的交点．解答本题要结合函数和方程的关系，关键是掌握二次函数y=ax2+bx+c系数符号的确定．
练习册系列答案
相关题目
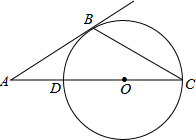如图，AC经过圆心O交⊙O于点D，AB与⊙O相切于点B．若∠A=x（0°＜x＜90°）∠C=y，则y与x之间的函数关系图象是（　　）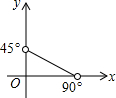
A、
B、
C、
D、
如图，数轴上有三个点A、B、C，表示的数分别是-4、-2、3，请回答：
（1）若将点B向左移动5个单位后，三个点所表示的数中，最小的数是
 
；
（2）若使C、B两点的距离与A、B两点的距离相等（A、C不重合），则需将点C向左移动
 
个单位；
（3）若移动A、B、C三点中的两个点，使三个点表示的数相同，移动方法有
 
种，其中移动所走的距离和最大的是
 
个单位；
（4）若在原点处有一只小青蛙，一步跳1个单位长．小青蛙第1次先向左跳1步，第2次再向右跳3步，然后第3次再向左跳5步，第4次再向右跳7步，…，按此规律继续跳下去，那么跳第100次时，应跳
 
步，落脚点表示的数是
 
；跳了第n次（n是正整数）时，落脚点表示的数是
 
．
（5）数轴上有个动点表示的数是x，则|x-2|+|x+3|的最小值是
 
．
如图是二次函数y1=ax2+bx+c和一次函数y2=mx+n的图象，观察图象，当ax2+（b-m）x+c-n=0时，求x的值．
下列五个命题
（1）若直角三角形的两条边长为5和12，则第三边长是13；
（2）如果a≥0，那么 (
a
)2=a；
（3）若点P在第三象限，则将点P绕原点顺时针旋转90°得P1（-b，a）；
（4）对角线互相垂直且相等的四边形是正方形；
（5）某校初三（2）有7名同学的体能测试成绩（单位：分）如下：50，48，47，50，48，49，48．这组数据的中位数和众数是分别48，50
其中不正确命题的个数是（　　）
A、4B、3C、2D、1
如图，在Rt△ABC中，∠C=90°，AC=5，AB=13，则cosB的值为（　　）
A、
5
13
B、
12
13
C、
5
12
D、
13
5
如图，线段AB两个端点的坐标分别是A（6，4），B（8，2），以原点O为位似中心，在第一象限内将线段AB缩小为原来的
1
2
后得到线段CD，则端点C的坐标为（　　）
A、（3，2）
B、（4，1）
C、（3，1）
D、（4，2）
已知正方形的对角线长为6，则此正方形的边长为
 
．
下列各式中正确的是（　　）
A、3÷
1
3
=1
B、(-
1
2
)÷(-
1
2
)=1
C、（-5）×0÷0=0
D、2÷3×(-
1
3
)=-2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网