题目内容
在△ABC中,∠A=70°,∠B,∠C的平分线交于点O,则∠BOC= 度.
考点:三角形内角和定理
专题:
分析:先利用角平分线的性质求出∠2+∠4的度数,再由三角形的内角和定理便可求出∠BOC的度数.
解答: 解:∵∠ABC和∠ACB的平分线BD、CE相交于点O,
解:∵∠ABC和∠ACB的平分线BD、CE相交于点O,
∴∠1=∠2,∠3=∠4,
∴∠2+∠4=
(180°-∠A)=
(180°-70°)=55°,
∴∠BOC=180°-(∠2+∠4)=180°-55°=125°.
故答案为:125.
 解:∵∠ABC和∠ACB的平分线BD、CE相交于点O,
解:∵∠ABC和∠ACB的平分线BD、CE相交于点O,∴∠1=∠2,∠3=∠4,
∴∠2+∠4=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=180°-(∠2+∠4)=180°-55°=125°.
故答案为:125.
点评:本题考查的是角平分线的性质及三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目
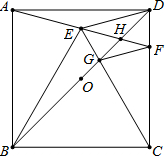 如图,正方形ABCD中,O为BD中点,以BC为边向正方形内部作等边△BCE,连接并延长AE交CD于F,连接BD分别交CE、AF于G、H,下列结论:
如图,正方形ABCD中,O为BD中点,以BC为边向正方形内部作等边△BCE,连接并延长AE交CD于F,连接BD分别交CE、AF于G、H,下列结论:①∠CEH=45°;②GF∥ED;③2OH+DH=BH;④BG=
| 2 |
| ||
| 2 |
其中正确的结论有( )
| A、5个 | B、4个 | C、3个 | D、2个 |
对于函数y=
,当自变量x=2.5时,对应的函数值是( )
| 2x-1 |
| A、2 | B、-2 | C、±2 | D、4 |
在菱形ABCD中,对角线AC与BD交于点O,如果∠ABC=60°,AC=4,那么该菱形的面积是( )
A、16
| ||
| B、16 | ||
C、8
| ||
| D、8 |