题目内容
 如图,在梯形ABCD中,AD∥BC,AB=AC,∠BAC=90°,AC与BD相交于O,BC=BD,求证:CD=CO.
如图,在梯形ABCD中,AD∥BC,AB=AC,∠BAC=90°,AC与BD相交于O,BC=BD,求证:CD=CO.考点:梯形,含30度角的直角三角形,等腰直角三角形
专题:证明题
分析:作AF⊥BC于F,DE⊥BC于E,根据等腰直角三角形的性质用AB表示出BC及AF的长,由锐角三角函数的定义求出∠1的度数,根据BC=BD得出∠BDC的度数,由三角形外角的性质得出∠DOC的度数,进而可得出结论.
解答: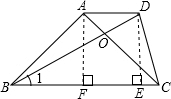 解:如图,作AF⊥BC于F,DE⊥BC于E,
解:如图,作AF⊥BC于F,DE⊥BC于E,
在Rt△ABC中,
∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∴BC=
AB,AF=
AB,
∴AF=
BC.
又∵DE=AF,
∴DE=
BC=
BD,
∴
=
,
∴sin∠1=
,
∴∠1=30°.
∵BC=BD,
∴∠BDC=∠BCD=
=75°,
∴∠DOC=∠1+∠ACB=30°+45°=75°=∠BDC,
∴DC=CO.
 解:如图,作AF⊥BC于F,DE⊥BC于E,
解:如图,作AF⊥BC于F,DE⊥BC于E,在Rt△ABC中,
∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∴BC=
| 2 |
| ||
| 2 |
∴AF=
| 1 |
| 2 |
又∵DE=AF,
∴DE=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| DE |
| BD |
| 1 |
| 2 |
∴sin∠1=
| 1 |
| 2 |
∴∠1=30°.
∵BC=BD,
∴∠BDC=∠BCD=
| 180°-30° |
| 2 |
∴∠DOC=∠1+∠ACB=30°+45°=75°=∠BDC,
∴DC=CO.
点评:本题考查了梯形及等腰三角形的判定,难度一般,关键是巧妙作辅助线进行解答.

练习册系列答案
相关题目
 如图,在平行四边形ABCD中,AE垂直于CD,E是垂足.如果∠B=55°,那么∠DAE的角度为( )
如图,在平行四边形ABCD中,AE垂直于CD,E是垂足.如果∠B=55°,那么∠DAE的角度为( )| A、25° | B、35° |
| C、45° | D、55° |
关于x的分式方程
=2+
会产生增根,则x的值为( )
| x |
| x-3 |
| k |
| x-3 |
| A、1 | B、2 | C、3 | D、4 |
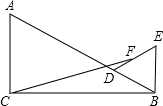 如图,Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=4,D为线段AB上一个动点,以BD为边在△ABC外作等边△BDE.若F为DE中点,则CF的最小值为
如图,Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=4,D为线段AB上一个动点,以BD为边在△ABC外作等边△BDE.若F为DE中点,则CF的最小值为 如图,在△ABC中,点D在BC上,BD=AD=AC,∠BAC=60°,求∠B的度数.
如图,在△ABC中,点D在BC上,BD=AD=AC,∠BAC=60°,求∠B的度数.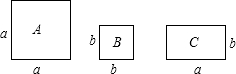 如图,正方形卡片A类、B类和长方形卡片C类各若干张(a≠b),如果要选用上述3类卡片共12张拼成一个大长方形(拼接时不可重叠,不可有缝隙)、且卡片全部用上,则不同的选取方案有
如图,正方形卡片A类、B类和长方形卡片C类各若干张(a≠b),如果要选用上述3类卡片共12张拼成一个大长方形(拼接时不可重叠,不可有缝隙)、且卡片全部用上,则不同的选取方案有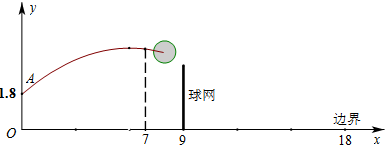
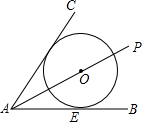 如图所示,已知PA是∠BAC的平分线,AB是⊙O的切线,切点为E,求证:AC是⊙O的切线.
如图所示,已知PA是∠BAC的平分线,AB是⊙O的切线,切点为E,求证:AC是⊙O的切线.