题目内容
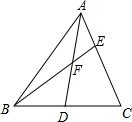 在△ABC中,D是△ABC的BC边上的中点,F是AD的中点,BF的延长线交AC于点E.求证:AE=
在△ABC中,D是△ABC的BC边上的中点,F是AD的中点,BF的延长线交AC于点E.求证:AE=| 1 |
| 2 |
考点:三角形中位线定理
专题:证明题
分析:如图,过点D作DM∥AC交BE于点M.利用平行线分线段成比例求得DM=AE;然后由三角形中位线定理推知DM=
EC,易证AE=
CE.
| 1 |
| 2 |
| 1 |
| 2 |
解答: 证明:如图,过点D作DM∥AC交BE于点M.
证明:如图,过点D作DM∥AC交BE于点M.
∵F是AD的中点,
∴DF=AF,
∴
=
=1,则AE=DM,
又∵点D是BC的中点,
∴DM是△BEC的中位线,
∴DM=
EC,
∴AE=
CE.
 证明:如图,过点D作DM∥AC交BE于点M.
证明:如图,过点D作DM∥AC交BE于点M.∵F是AD的中点,
∴DF=AF,
∴
| DM |
| AE |
| DF |
| AF |
又∵点D是BC的中点,
∴DM是△BEC的中位线,
∴DM=
| 1 |
| 2 |
∴AE=
| 1 |
| 2 |
点评:此题考查的是三角形中位线的性质,即三角形的中位线平行于第三边且等于第三边的一半.

练习册系列答案
相关题目
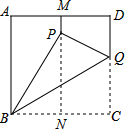 如图所示,正方形纸片ABCD的边长为1,M,N分别是AD,BC的中点,将点C折叠到MN上,落在点P的位置,折痕为BQ.连结QP,PB,求PN,MP和CQ的长.
如图所示,正方形纸片ABCD的边长为1,M,N分别是AD,BC的中点,将点C折叠到MN上,落在点P的位置,折痕为BQ.连结QP,PB,求PN,MP和CQ的长.
 已知AC、CD分别切⊙O于A、D两点,连接BD.
已知AC、CD分别切⊙O于A、D两点,连接BD. 如图,在△ABC中,AB=AC,D是BC边上的中点,且DE⊥AB,DF⊥AC.
如图,在△ABC中,AB=AC,D是BC边上的中点,且DE⊥AB,DF⊥AC.