题目内容
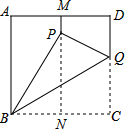 如图所示,正方形纸片ABCD的边长为1,M,N分别是AD,BC的中点,将点C折叠到MN上,落在点P的位置,折痕为BQ.连结QP,PB,求PN,MP和CQ的长.
如图所示,正方形纸片ABCD的边长为1,M,N分别是AD,BC的中点,将点C折叠到MN上,落在点P的位置,折痕为BQ.连结QP,PB,求PN,MP和CQ的长.考点:翻折变换(折叠问题)
专题:
分析:由中点的定义可得BN=
,折叠的性质可得BP=BC=1,在Rt△BPN中,根据勾股定理求PN的值,即可求得MP;由折叠的性质知∠BPQ=∠C=90°,利用直角三角形中的cos∠PBN=BN:PB=1:2,可求得∠PBN=60°,∠PBQ=30°,从而求出CQ=PQ=PBtan30°.
| 1 |
| 2 |
解答:解:∵ABCD是正方形,M、N分别为AD、BC的中点,
∴ABNM是矩形,BN=
BC=
,
∵BP=BC=1(折叠的性质),
在Rt△BPN中,
PN=
=
,
∴MP=MN-PN=1-
;
∵∠CBQ=∠PBQ=
∠PBC,BC=PB=2BN=1,∠BPQ=∠C=90°
∴cos∠PBN=BN:PB=1:2
∴∠PBN=60°,∠PBQ=30°
∴CQ=PQ=PBtan30°=
.
∴ABNM是矩形,BN=
| 1 |
| 2 |
| 1 |
| 2 |
∵BP=BC=1(折叠的性质),
在Rt△BPN中,
PN=
| BP2-BN2 |
| ||
| 2 |
∴MP=MN-PN=1-
| ||
| 2 |
∵∠CBQ=∠PBQ=
| 1 |
| 2 |
∴cos∠PBN=BN:PB=1:2
∴∠PBN=60°,∠PBQ=30°
∴CQ=PQ=PBtan30°=
| ||
| 3 |
点评:考查了翻折变换(折叠问题),本题利用了:1、折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;2、正方形的性质,直角三角形的性质,锐角三角函数的概念求解.

练习册系列答案
相关题目
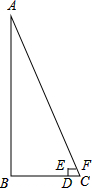 兴趣小组的同学要测量树的高度,在阳光下,一名同学测得一根长为1m的竹竿的影长为0.4m,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼第一级台阶上,并测得台阶上的影子长为0.2m,一级台阶高为0.3m,如图所示,其中AB为树高,EF为树影在第一级台阶上的影长,BD为树影在地面上部分的长,ED的长为台阶高.若这棵树落在地面上的影长为4.4m,则树高为多少米?
兴趣小组的同学要测量树的高度,在阳光下,一名同学测得一根长为1m的竹竿的影长为0.4m,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼第一级台阶上,并测得台阶上的影子长为0.2m,一级台阶高为0.3m,如图所示,其中AB为树高,EF为树影在第一级台阶上的影长,BD为树影在地面上部分的长,ED的长为台阶高.若这棵树落在地面上的影长为4.4m,则树高为多少米?
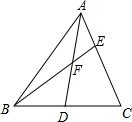 在△ABC中,D是△ABC的BC边上的中点,F是AD的中点,BF的延长线交AC于点E.求证:AE=
在△ABC中,D是△ABC的BC边上的中点,F是AD的中点,BF的延长线交AC于点E.求证:AE=