题目内容
 如图,已知OB平分∠AOC,且∠2:∠3:∠4=1:3:4,求∠1、∠3、∠4的度数.
如图,已知OB平分∠AOC,且∠2:∠3:∠4=1:3:4,求∠1、∠3、∠4的度数.分析:求出∠1:∠2:∠3:∠4=1:1:3:4,设∠1=x°,∠2=x°,∠3=3x°,∠4=4x°,得出方程x+x+3x+4x=360,求出x=40,即可求出答案.
解答:解:∵OB平分∠AOC,
∴∠1=∠2,
∵∠2:∠3:∠4=1:3:4,
∴∠1:∠2:∠3:∠4=1:1:3:4,
设∠1=x°,∠2=x°,∠3=3x°,∠4=4x°,
则x+x+3x+4x=360,
x=40,
即∠1=40°,3=120°,4=160°.
∴∠1=∠2,
∵∠2:∠3:∠4=1:3:4,
∴∠1:∠2:∠3:∠4=1:1:3:4,
设∠1=x°,∠2=x°,∠3=3x°,∠4=4x°,
则x+x+3x+4x=360,
x=40,
即∠1=40°,3=120°,4=160°.
点评:本题考查了角的有关计算和角的平分线定义的应用,主要考查学生的计算能力,用了方程思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 15、阅读材料:如图,已知OB平分∠ABD,OC平分∠ACD,问:∠A、∠D、∠O之间是否存在某种确定的数量关系.
15、阅读材料:如图,已知OB平分∠ABD,OC平分∠ACD,问:∠A、∠D、∠O之间是否存在某种确定的数量关系. 如图,已知OB平分∠AOC,OD平分∠COE,∠AOE=140°,∠COD=30°,求∠AOB的度数.
如图,已知OB平分∠AOC,OD平分∠COE,∠AOE=140°,∠COD=30°,求∠AOB的度数. 如图,已知OB平分∠AOC,OD平分∠COE,∠AOD=110°,∠BOE=100°,求∠AOE的度数.
如图,已知OB平分∠AOC,OD平分∠COE,∠AOD=110°,∠BOE=100°,求∠AOE的度数.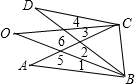 定的数量关系.
定的数量关系.