Question

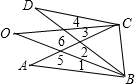
15、阅读材料：如图，已知OB平分∠ABD，OC平分∠ACD，问：∠A、∠D、∠O之间是否存在某种确定的数量关系．
解：由三角形内角和等于180°，得
∠A+∠1=180°-∠5
∠O+∠3=180°-∠6
∴∠A+∠1=∠O+∠3        ①
同理可得：∠D+∠4=∠O+∠2  ②
由式子①和②可知，∠A、∠D、∠O之间的一个确定的数量关系为 2∠O．

Answer 1

分析：本题已知的条件是角平分线，根据角平分线与三角形的内角和定理，理解阅读材料，观察式子①和②当中的∠1，∠2，∠3，∠4之间的关系，通过两式消去这四个角就可以得到，∠A、∠D、∠O之间的一个确定的数量关系．

解答：解：∵OB平分∠ABD，OC平分∠ACD，
∴∠1=∠2，∠3=∠4，
再将式子①和②相加得：
∠A+∠D=∠O；
所以，∠A、∠D、∠O之间的一个确定的数量关系为∠A+∠D=∠O．

点评：阅读问题，注重每步的依据，体会消元的方法是加减法或代入法．