题目内容
点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.利用数形结合思想回答下列问题:

(1)数轴上表示1和5两点之间的距离是 ,(2分)数轴上表示2和-1的两点之间的距离是 ;(2分)
(2)数轴上表示 和-1的两点之间的距离表示为 ;(2分)
和-1的两点之间的距离表示为 ;(2分)
(3)若 表示一个有理数,且
表示一个有理数,且 ,则
,则 ;(2分)
;(2分)
(4)利用数轴求出 的最小值,并写出此时
的最小值,并写出此时 可取哪些整数值?(4 分)
可取哪些整数值?(4 分)

(1)4 ;3; (2)|x+1| (3) 6(4) 最小值为7;此时x可取整数为-3,-2,-1,0,1,2,3,4.
【解析】
试题分析:(1)根据两点间距离公式求解即可;
(2)根据已知给出的求两点间距离的公式表示即可;
(3)根据x的取值范围,分别判断x-2与x+4的正负,然后根据绝对值的性质求解即可;
(4) 表示有理数x的点到-4及到3的距离之和,从而得到x的取值范围.
表示有理数x的点到-4及到3的距离之和,从而得到x的取值范围.
试题解析:(1)数轴上表示1和5两点之间的距离是|1-5|=4,数轴上表示2和-1的两点之间的距离是|2-(-1)|=3;
(2)数轴上表示 和-1的两点之间的距离表示为|x-(-1)|=|x+1|;
和-1的两点之间的距离表示为|x-(-1)|=|x+1|;
(3)∵
∴x-2<0,x+4>0
∴ -(x-2)+x+4=-x+2+x+4=6;
-(x-2)+x+4=-x+2+x+4=6;
(4) 表示有理数x的点到-4及到3的距离之和,所以当-3≤x≤4时,它取得最小值为7.
表示有理数x的点到-4及到3的距离之和,所以当-3≤x≤4时,它取得最小值为7.
此时x可取整数为-3,-2,-1,0,1,2,3,4
考点:1.数轴;2.绝对值;3.两点间的距离.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 的两个解恰好分别是等腰△ABC的底边长和腰长,则△ABC的周长为( )
的两个解恰好分别是等腰△ABC的底边长和腰长,则△ABC的周长为( ) ,
, ,0,
,0, ,
, ,
, ,
, ,
, ,则无理数有 ;分数有 .
,则无理数有 ;分数有 . B.
B. 与
与 C.
C. 与
与 D.
D. 与
与
 的图象上有两点(3,a)和(-5,a),则此拋物线的对称轴是( )
的图象上有两点(3,a)和(-5,a),则此拋物线的对称轴是( ) B.直线
B.直线 C.直线
C.直线 D.直线
D.直线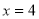


 B.8 C.
B.8 C. D.
D.