��Ŀ����
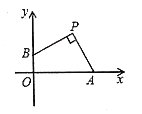
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���![]() ������Ϊ
������Ϊ![]() ����
����![]() ��
��![]() ����������ϣ����߶�
����������ϣ����߶�![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת90���õ�
˳ʱ����ת90���õ�![]() ������
������![]() ��
��![]() ��Ĵ��ߣ�����Ϊ
��Ĵ��ߣ�����Ϊ![]() ������
������![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��
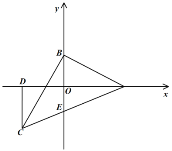
��1������![]() �ڵ�������ʱ����ʵ��
�ڵ�������ʱ����ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2���ڣ�1���������£���![]() ����
����![]() ȡ�����ֵʱ����ͼ��
ȡ�����ֵʱ����ͼ��![]() ����Ķ��κ���
����Ķ��κ���![]() �Ľ���ʽ��
�Ľ���ʽ��
��3���ڣ�2���������£���ֱ��![]() ����ƽ��
����ƽ��![]() ����λ������κ���
����λ������κ���![]() ��ͼ��ĺ�����Ϊ
��ͼ��ĺ�����Ϊ![]() ����
����![]() ����
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
���𰸡���1��![]() ����2��
����2��![]() ����3��
����3��![]() ��
��
��������
��1������B����ƽ��m����λ����ʱ��A�䣨6����m��������ʱ��AB�Ƶ�B˳ʱ����ת90��õ���C�䣨��m����6��������C������ƽ��m�ĵ�λ�õ���C����m��m��6����������⣻
��2��S��S��ABO+S��ADC��![]() ��AO��BO+
��AO��BO+![]() ��AD��CD��
��AD��CD��![]() ��6��m+
��6��m+![]() ����6+m������6��m������
����6+m������6��m������![]() m2+3m+18����S�����ֵ����ʱ��m��3��������⣻
m2+3m+18����S�����ֵ����ʱ��m��3��������⣻
��3�������Ľ���ĺ�����Ϊx0����x0�ݩ�3����x����3ʱ����������ֱ�ߵ��Ϸ���������⣮
�⣺��1������B����ƽ��m����λ����ʱ��A�䣨6����m��������ʱ��AB�Ƶ�B˳ʱ����ת90��õ���C�䣨��m����6����
����C������ƽ��m�ĵ�λ�õ���C����m��m��6����
��C�ڵ�������ʱ����m��0��m��6��0��
��ã�0��m��6��
��2��S��S��ABO+S��ADC��![]() ��AO��BO+
��AO��BO+![]() ��AD��CD��
��AD��CD��![]() ��6��m+
��6��m+![]() ����6+m������6��m������
����6+m������6��m������![]() m2+3m+18��
m2+3m+18��
�ߩ�![]() ��0����S�����ֵ����ʱ��m��3��
��0����S�����ֵ����ʱ��m��3��
�ʵ�C����3����3������A��6��0����
����C��A���������һ�κ�������ʽ����ã�
ֱ��AC�ı���ʽΪ��y��![]() x��2���ʵ�E��0����2����
x��2���ʵ�E��0����2����
��c����2������A��������������߱���ʽ�ã�0��36a��6��2����ã�a��![]() ��
��
�������ߵı���ʽΪ��y��![]() x2��x��2������
x2��x��2������
��3��ֱ��y����2��k��x+2����ƽ��k����λ��õ�����Ϊ��y����2��k��x+2+2������
�����٢��������ã�![]() x2����3��k��x��4��k��0��
x2����3��k��x��4��k��0��
������3��k��2+![]() ��4+k����k2��
��4+k����k2��![]() k+
k+![]() ��0��
��0��
����������ֱ�����������㣬
����ĺ�����Ϊx0����x0�ݩ�3����x����3ʱ����������ֱ�ߵ��Ϸ���
��x����3ʱ��y��![]() x2��x��2��3��
x2��x��2��3��
��x����3ʱ��y����2��k��x+2+2��4k��4��
��4k��4��3��
��ã�k��![]() ��
��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�