题目内容
 为了促进节能减排,倡导节约用电,某市将实行居民生活用电阶梯电价方案,图中折线反映了每户每月用电电费y(元)与用电量x(度)间的函数关系.在每月用电量超过230度时,每多用1度电要比第二档多付电费m元,小刚家某月用电290度,交电费153元,则m=
为了促进节能减排,倡导节约用电,某市将实行居民生活用电阶梯电价方案,图中折线反映了每户每月用电电费y(元)与用电量x(度)间的函数关系.在每月用电量超过230度时,每多用1度电要比第二档多付电费m元,小刚家某月用电290度,交电费153元,则m=考点:一次函数的应用
专题:
分析:分别求出第二、三档每度电的费用,进而得出m的值即可.
解答:解:根据图象可得出:
用电230度,需要付费108元,用电140度,需要付费63元,
∵108-63=45(元),
230-140=90(度),
∴45÷90=0.5(元),
∴第二档电费为0.5元/度;
∵小刚家某月用电290度,交电费153元,
290-230=60(度),153-108=45(元),
∴45÷60=0.75(元),
∴m=0.75-0.5=0.25元,
故答案为0.25元.
用电230度,需要付费108元,用电140度,需要付费63元,
∵108-63=45(元),
230-140=90(度),
∴45÷90=0.5(元),
∴第二档电费为0.5元/度;
∵小刚家某月用电290度,交电费153元,
290-230=60(度),153-108=45(元),
∴45÷60=0.75(元),
∴m=0.75-0.5=0.25元,
故答案为0.25元.
点评:本题主要考查了一次函数的应用以及待定系数法求一次函数解析式的运用,在解答本题时利用图象获取正确信息是解题关键.

练习册系列答案
相关题目
 如图,菱形ABCD的两条对角线相交于O,若菱形的周长为20,AC=8,则菱形的面积是( )
如图,菱形ABCD的两条对角线相交于O,若菱形的周长为20,AC=8,则菱形的面积是( )| A、24 | B、48 | C、12 | D、40 |
为了解某区九年级学生课外体育活动的情况,从该年级学生中随机抽取了4%的学生,对其参加的体育活动项目进行了调查,将调查的数据进行统计并绘制了扇形图和条形图.下列结论错误的是( )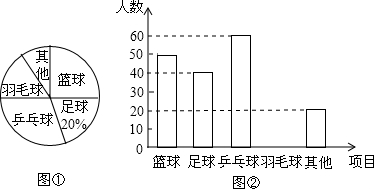

| A、被抽测学生中参加其他体育项目活动人数占10% |
| B、被抽测学生中参加羽毛球项目人数为30人 |
| C、估计全区九年级参加篮球项目的学生比参加足球项目的学生多20% |
| D、全区九年级大约有1500名学生参加乒乓球项目 |
若P为质数,且P2+13仍为质数,则P3+25为( )
| A、质数 | B、合数 |
| C、能为质数,也可能为合数 | D、无法确定 |