题目内容
（2013•抚顺）在与水平面夹角是30°的斜坡的顶部，有一座竖直的古塔，如图是平面图，斜坡的顶部CD是水平的，在阳光的照射下，古塔AB在斜坡上的影长DE为18米，斜坡顶部的影长DB为6米，光线AE与斜坡的夹角为30°，求古塔的高（| 2 |
| 3 |
分析：延长BD交AE于点F，作FG⊥ED于点G，Rt△FGD中利用锐角三角函数求得FD的长，从而求得FB的长，然后在直角三角形ABF中利用锐角三角函数求得AB的长即可．
解答：
解：延长BD交AE于点F，作FG⊥ED于点G，
∵斜坡的顶部CD是水平的，斜坡与地面的夹角为30°，
∴∠FDE=∠AED=30°，
∴FD=FE，
∵DE=18米，
∴EG=GD=
ED=9米，
在Rt△FGD中，
DF=
=
=6
米，
∴FB=（6
+6）米，
在Rt△AFB中，
AB=FB•tan60°=（6
+6）×
=（18+6
）≈28.2米，
所以古塔的高约为28.2米．
解：延长BD交AE于点F，作FG⊥ED于点G，∵斜坡的顶部CD是水平的，斜坡与地面的夹角为30°，
∴∠FDE=∠AED=30°，
∴FD=FE，
∵DE=18米，
∴EG=GD=
| 1 |
| 2 |
在Rt△FGD中，
DF=
| DG |
| cos30° |
| 9 | ||||
|
| 3 |
∴FB=（6
| 3 |
在Rt△AFB中，
AB=FB•tan60°=（6
| 3 |
| 3 |
| 3 |
所以古塔的高约为28.2米．
点评：此题主要考查了解直角三角形的应用，解决本题的难点是把塔高的影长分为在平地和斜坡上两部分．
练习册系列答案
目标测试系列答案
相关题目
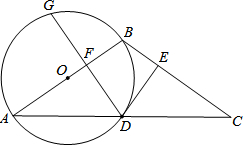（2013•抚顺）如图，在△ABC中，AB=BC，以AB为直径的⊙O交AC于点D，DE⊥BC，垂足为E．