题目内容
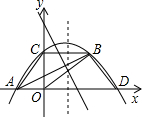
 已知如图,∠1+∠2=180°,∠3=100°,OK平分∠DOH,则∠KOH=________度.
已知如图,∠1+∠2=180°,∠3=100°,OK平分∠DOH,则∠KOH=________度.
40
分析:由于∠1+∠2=180°,根据同旁内角互补,两直线平行得到AB∥CD,再利用平行线的性质得到∠GOD=∠3=100°,则∠HOD=80°,然后利用角平分线的定义得到∠KOH= ∠HOD=
∠HOD= ×80°=40°.
×80°=40°.
解答:∵∠1+∠2=180°,
∴AB∥CD,
∴∠GOD=∠3=100°,
∴∠HOD=180°-100°=80°,
∵OK平分∠DOH,
∴∠KOH= ∠HOD=
∠HOD= ×80°=40°.
×80°=40°.
故答案为40.
点评:本题考查了平行线的判定与性质:同旁内角互补,两直线平行;两直线平行,同位角相等.也考查了角平分线的定义.
分析:由于∠1+∠2=180°,根据同旁内角互补,两直线平行得到AB∥CD,再利用平行线的性质得到∠GOD=∠3=100°,则∠HOD=80°,然后利用角平分线的定义得到∠KOH=
 ∠HOD=
∠HOD= ×80°=40°.
×80°=40°.解答:∵∠1+∠2=180°,
∴AB∥CD,
∴∠GOD=∠3=100°,
∴∠HOD=180°-100°=80°,
∵OK平分∠DOH,
∴∠KOH=
 ∠HOD=
∠HOD= ×80°=40°.
×80°=40°.故答案为40.
点评:本题考查了平行线的判定与性质:同旁内角互补,两直线平行;两直线平行,同位角相等.也考查了角平分线的定义.

练习册系列答案
相关题目
已知如图,点C是线段AB的黄金分割点(AC>BC),则下列结论中正确的是( )


| A、AB2=AC2+BC2 | ||||||
| B、BC2=AC•BA | ||||||
C、
| ||||||
D、
|
 过△ABC的三个顶点,
过△ABC的三个顶点,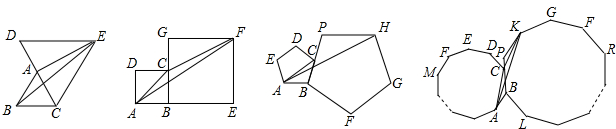
 (2012•通州区一模)已知如图,在△ABC中,AB=AC,∠ABC=α,将△ABC以点B为中心,沿逆时针方向旋转α度(0°<α<90°),得到△BDE,点B、A、E恰好在同一条直线上,连接CE.
(2012•通州区一模)已知如图,在△ABC中,AB=AC,∠ABC=α,将△ABC以点B为中心,沿逆时针方向旋转α度(0°<α<90°),得到△BDE,点B、A、E恰好在同一条直线上,连接CE. 已知如图,菱形ABCD中,∠ADC=120°,BD=2
已知如图,菱形ABCD中,∠ADC=120°,BD=2