题目内容
3.式子$\frac{{\sqrt{a+1}}}{a-2}$有意义,则实数a的取值范围是( )| A. | a≥-1 | B. | a≠2 | C. | a≥-1且a≠2 | D. | a>2 |
分析 直接利用二次根式的定义结合分式有意义的条件分析得出答案.
解答 解:式子$\frac{{\sqrt{a+1}}}{a-2}$有意义,
则a+1≥0,且a-2≠0,
解得:a≥-1且a≠2.
故选:C.
点评 此题主要考查了二次根式有意义的条件,正确把握定义是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.某种股票原价格为a元,连续两天上涨,每次涨幅10%,则该股票两天后的价格为( )
| A. | 1.21a元 | B. | 1.1a元 | C. | 1.2a元 | D. | (0.2+a) 元 |
18.-3的绝对值是( )
| A. | -3 | B. | 3 | C. | ±3 | D. | $\frac{1}{3}$ |
8.观察下面“品”字形中各数之间的规律,根据观察到的规律得出a的值为( )


| A. | 23 | B. | 75 | C. | 77 | D. | 139 |
15.肥皂泡的泡壁厚度大约是0.00000071米,数字0.00000071用科学记数法表示为( )
| A. | 7.1×107 | B. | 0.71×10-6 | C. | 7.1×10-7 | D. | 71×10-8 |
12.计算(-3)+5的结果等于( )
| A. | 2 | B. | -2 | C. | 8 | D. | -8 |
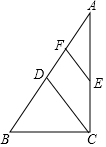 如图,在Rt△ABC中,∠ACB=90°,点D,E分别是AB,AC的中点,点F是AD的中点.若AB=8,则EF=2.
如图,在Rt△ABC中,∠ACB=90°,点D,E分别是AB,AC的中点,点F是AD的中点.若AB=8,则EF=2.