Question

9．已知等腰三角形的腰长为10，一腰上的高为6，求以底边为边长的正方形的面积．

Answer 1

分析 分两种情况：①当等腰三角形为锐角三角形时；②当等腰三角形为钝角三角形时；由勾股定理求出AD，再由勾股定理求出BC²，即可得出结果．

解答 解：分两种情况：
①当等腰三角形为锐角三角形时，如图1所示：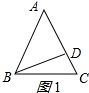
∵AB=AC=10，BD是AC边上的高，
∴∠ADB=∠CDB=90°，
∴AD=$\sqrt{{AB}^{2}-B{D}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8，
∴CD=10-8=2，
∴BC²=BD²+CD²=6²+2²=40，
即以底边为边长的正方形的面积为40；
（2）当等腰三角形为钝角三角形时，如图2所示：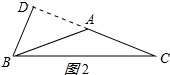
∵AB=AC=10，BD是AC边上的高，
∴∠ADB=90°，
∴AD=$\sqrt{{AB}^{2}-B{D}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8，
∴CD=10+8=18，
∴BC²=BD²+CD²=6²+18²=360，
即以底边为边长的正方形的面积为360．

点评 本题考查了勾股定理、等腰三角形的性质、正方形面积的计算；熟练掌握勾股定理，并能进行推理计算是解决问题的关键．