题目内容
20. 如图,点B、D、C、F在一条直线上,且AB∥EF,AC∥DE,求证:△ABC∽△EFD.
如图,点B、D、C、F在一条直线上,且AB∥EF,AC∥DE,求证:△ABC∽△EFD.
分析 由AB∥EF,AC∥DE,根据两直线平行,内错角相等,可求得∠B=∠F,∠ACB=∠EDF,然后由有两组角对应相等的两个三角形相似,证得结论.
解答 证明:∵AB∥EF,AC∥DE,
∴∠B=∠F,∠ACB=∠EDF,
∴△ABC∽△EFD.
点评 此题考查了相似三角形的判定以及平行线的性质.注意有两组角对应相等的两个三角形相似.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.在△ABC中,A,B都是锐角,且sinA=$\frac{\sqrt{3}}{2}$,tanB=$\sqrt{3}$,AB=8,则AB边上的高为( )
| A. | 4$\sqrt{3}$ | B. | 8$\sqrt{3}$ | C. | 16$\sqrt{3}$ | D. | 24$\sqrt{3}$ |
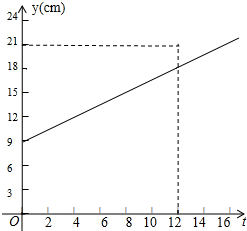 某种植物生长t天的高度为y厘米,如图反映了y与t之间的函数关系,请根据图象回答问题:
某种植物生长t天的高度为y厘米,如图反映了y与t之间的函数关系,请根据图象回答问题: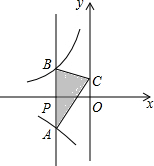 如图,过x轴负半轴上的任意一点P,作y轴的平行线,分别与反比例函数y=$\frac{-6}{x}$,y=$\frac{4}{x}$交于A,B两点.若点C是y轴上任意一点,连接AC,BC,则△ABC的面积是5.
如图,过x轴负半轴上的任意一点P,作y轴的平行线,分别与反比例函数y=$\frac{-6}{x}$,y=$\frac{4}{x}$交于A,B两点.若点C是y轴上任意一点,连接AC,BC,则△ABC的面积是5.