题目内容
14．已知在Rt△ABC中，∠ACB=90°，AC=6，BC=8，以点C为圆心，r为半径作圆．（1）要使点A在⊙C内，点B在⊙C外，求半径r的取值范围；
（2）要使⊙C与AB相切，求半径r．
分析 （1）根据d＞r时，点在圆外；当d=r时，点在圆上；当d＜r时，点在圆内，可得答案；
（2）根据圆心到直线的距离等于半径时直线与圆相切，可得答案，
解答 解：（1）由点A在⊙C内，点B在⊙C外，得
6＜r＜8；
（2）由勾股定理，得
AB=10，
C到AB的距离为$\frac{6×8}{10}$=$\frac{24}{5}$，
r=$\frac{24}{5}$时，⊙C与AB相切．
点评 本题考查了点与圆的位置关系，d＞r时，点在圆外；当d=r时，点在圆上；当d＜r时，点在圆内．
练习册系列答案
相关题目
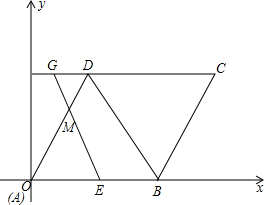如图，菱形ABCD的顶点A与平面直角坐标系中的点O重合，AB在X轴上，其边长为6cm，∠DAB=60°，点M是AD一点，且DM=2cm，点E、F分别从A、D两点同时出发，E点以每秒1cm的速度沿A→B向B点运动，F点以每秒⒉5cm的速度沿D→C→B→A运动．当一点到达终点时，另一点立即停止运动．EM、CD的延长线相交于点G．
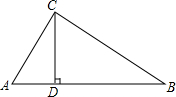如图，在Rt△ABC中，∠ACB=90°，作CD⊥AB于点D，
已知△ABC中，AC=6cm，BC=8cm，AB=10cm，CD为AB边上的高．动点P从点A出发，沿着△ABC的三条边逆时针走一圈回到A点，速度为2cm/s，设运动时间为ts．