题目内容
已知：
=
；
=
；
计算：
= ；
猜想：
= ．
| 2-1 |
| 22-12 |
| 1 |
| 3 |
| 4-3+2-1 |
| 42-32+22-12 |
| 1 |
| 5 |
计算：
| 6-5+4-3+2-1 |
| 62-52+42-32+22-12 |
猜想：
| [(2n+2)-(2n+1)]+…+(6-5)+(4-3)+(2-1) |
| [(2n+2)2-(2n+1)2]+…+(62-52)+(42-32)+(22-12) |
考点：规律型：数字的变化类
专题：规律型
分析：由
=
；
=
；
=
；…
由此看出分子是从n个1相加，结果等于n；分母是（4n+3）+（4n-1）+…+11+7+3=
=n（2n+3），故猜想
=
．
| 2-1 |
| 22-12 |
| 1 |
| 3 |
| 4-3+2-1 |
| 42-32+22-12 |
| 1 |
| 5 |
| 6-5+4-3+2-1 |
| 62-52+42-32+22-12 |
| 1 |
| 7 |
由此看出分子是从n个1相加，结果等于n；分母是（4n+3）+（4n-1）+…+11+7+3=
| n(4n+3+3) |
| 2 |
| [(2n+2)-(2n+1)]+…+(6-5)+(4-3)+(2-1) |
| [(2n+2)2-(2n+1)2]+…+(62-52)+(42-32)+(22-12) |
| 1 |
| 2n+3 |
解答：解：已
=
；
=
；
=
；
…
分子为n个1相加，结果等于n；
分母为n项相加：（4n+3）+（4n-1）+…+11+7+3=
=n（2n+3）
∴猜想
=
=
．
故答案为：
；
．
| 2-1 |
| 22-12 |
| 1 |
| 3 |
| 4-3+2-1 |
| 42-32+22-12 |
| 1 |
| 5 |
| 6-5+4-3+2-1 |
| 62-52+42-32+22-12 |
| 1 |
| 7 |
…
| [(2n+2)-(2n+1)]+…+(6-5)+(4-3)+(2-1) |
| [(2n+2)2-(2n+1)2]+…+(62-52)+(42-32)+(22-12) |
分子为n个1相加，结果等于n；
分母为n项相加：（4n+3）+（4n-1）+…+11+7+3=
| n(4n+3+3) |
| 2 |
∴猜想
| [(2n+2)-(2n+1)]+…+(6-5)+(4-3)+(2-1) |
| [(2n+2)2-(2n+1)2]+…+(62-52)+(42-32)+(22-12) |
| n |
| n(2n+3) |
| 1 |
| 2n+3 |
故答案为：
| 1 |
| 7 |
| 1 |
| 2n+3 |
点评：此题考查数字的变化规律，找出数字之间的运算规律，利用规律解决问题．
练习册系列答案
相关题目
如图，在Rt△ABC中，∠ABC=90°，AB=3，AC=5，点E在BC上，将△ABC沿AE折叠，使点B落在AC边上的点B′处，则BE的长为
如图，在五边形ABCDE中，若∠D=95°，则∠1+∠2+∠3+∠4=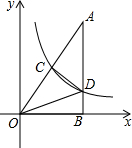
如图，Rt△AOB的一条直角边OB在x轴上，双曲线y=