Question

已知：如图，BD是⊙O的直径，过圆上一点A作⊙O的切线交DB的延长线于P，过B点作BC∥PA交⊙O于C，连接AB、AC．
（1）求证：AB=AC；
（2）若PA=10，PB=5，求⊙O的半径和AC的长．

Answer 1

分析：（1）根据弦切角定理得到∠1=∠C和平行线的性质定理得到∠1=∠2，则∠2=∠C，从而证明结论；
（2）根据切割线定理即可求得圆的半径，要求AC的长，只需求得AB的长．根据直角三角形的勾股定理和AB：AD的值联立求解．

解答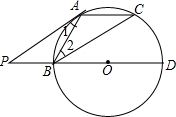：（1）证明：∵BC∥AP
∴∠1=∠2
∵PA切圆于点A
∴∠1=∠C
∴∠2=∠C
∴AB=AC

（2）解：∵PA²=PB•PD
即10²=5×（5+2×OB）
∴OB=

15

2

，∴⊙O的半径为7.5
∵PDA∽△PAB
∴

AD

AB

=

PA

PB

=

10

5

=2
∵BD²=AB²+AD²，即15²=AB²+（2AB）²
∴AB=3

5

，即AC=3

5

．

点评：此题综合运用了弦切角定理、切割线定理、相似三角形的性质和勾股定理．