题目内容
若方程4x2+8x-1=0的两根是x1=
,x2=
,则二次三项式4x2+8x-1可分解因式为( )
-2+
| ||
| 2 |
-2-
| ||
| 2 |
A、4(x-
| ||||||||
B、(x+
| ||||||||
C、4(x+
| ||||||||
D、(2x+2-
|
考点:解一元二次方程-因式分解法
专题:计算题
分析:由于4x2+8x-1=0可化为x2+2x-1=0,则x2+2x-1=0的两根为x1=
,x2=
,可得到x2+2x-1=(x-
)(x-
)=0,所以4x2+8x-1=4(x-
)(x-
).
-2+
| ||
| 2 |
-2-
| ||
| 2 |
-2+
| ||
| 2 |
-2-
| ||
| 2 |
-2+
| ||
| 2 |
-2-
| ||
| 2 |
解答:解:∵4x2+8x-1=0的两根是x1=
,x2=
,
∴4x2+8x-1=4(x-
)(x-
).
故选A.
-2+
| ||
| 2 |
-2-
| ||
| 2 |
∴4x2+8x-1=4(x-
-2+
| ||
| 2 |
-2-
| ||
| 2 |
故选A.
点评:本题考查了解一元二次方程-因式分解法:先把方程右边变形为0,再把方程左边分解为两个一次式的乘积,这样原方程转化为两个一元一次方程,然后解一次方程即可得到一元二次方程的解.

练习册系列答案
相关题目
 如图,梯形ABCD中AB∥CD,∠DAB=90°,AB=4CD,E是腰BC上一点,CE=CD,过点E作EF⊥BC交AD于点F,若F是AD的中点,则下列结论:
如图,梯形ABCD中AB∥CD,∠DAB=90°,AB=4CD,E是腰BC上一点,CE=CD,过点E作EF⊥BC交AD于点F,若F是AD的中点,则下列结论:①AE⊥DE;②AB=AD;③tan∠EFD=
| 4 |
| 3 |
其中正确结论的个数是( )
| A、4个 | B、3个 | C、2个 | D、1个 |
抛物线y=x2+bx+c与y轴交于A点,与x轴的正半轴交于B、C两点,且BC=2,S△ABC=3,则b的值为( )
| A、-5 | B、4或-4 | C、4 | D、-4 |
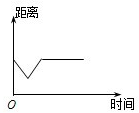
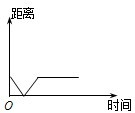
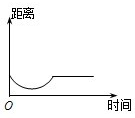
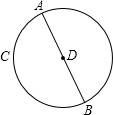 如图,在某度假旅游景区内,一艘旅游船先从A点沿⊙D的直径AB行驶到圆上的点B,然后从B点沿弧
如图,在某度假旅游景区内,一艘旅游船先从A点沿⊙D的直径AB行驶到圆上的点B,然后从B点沿弧
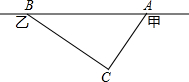 在甲村至乙村的公路有一块山地正在开发.现有一C处需要爆破.已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示.为了安全起见,爆破点C周围半径250米范围内不得进入,问在进行爆破时,公路AB段是否有危险,是否需要暂时封锁?请通过计算进行说明.
在甲村至乙村的公路有一块山地正在开发.现有一C处需要爆破.已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示.为了安全起见,爆破点C周围半径250米范围内不得进入,问在进行爆破时,公路AB段是否有危险,是否需要暂时封锁?请通过计算进行说明. 在如图所示的网格中,已知A(2,4),B(4,2),点C是第一象限内的一个格点,由点C与线段AB组成一个以AB为底,且腰长为无理数的等腰三角形.
在如图所示的网格中,已知A(2,4),B(4,2),点C是第一象限内的一个格点,由点C与线段AB组成一个以AB为底,且腰长为无理数的等腰三角形.
 如图,已知:AC=DF,BC=EF,AD=BE,你能判定BC∥EF吗?说说你的理由.
如图,已知:AC=DF,BC=EF,AD=BE,你能判定BC∥EF吗?说说你的理由.