题目内容
（1）∵AB∥______（已知）
∴∠ABC=∠1______
（2）∵∠ADE=∠B（已知）
∴DE∥______
∴∠CED+∠C=180°______．
解：（1）∵AB∥CD，
∴∠ABC=∠1；
（2）∵∠ADE=∠B，
∴DE∥BC，
∴∠CED+∠C=180°．
故答案为CD，（两直线平行，内错角相等）；BC，两直线平行，同旁内角互补．
分析：（1）根据两直线平行，内错角相等得到要使∠ABC=∠1，则AB∥CD；
（2）根据同位角相等两直线平行得到DE∥BC，再根据两直线平行，同旁内角互补得到∠CED+∠C=180°．
点评：本题考查了直线平行的判定与性质：同位角相等两直线平行；两直线平行，内错角相等；两直线平行，同旁内角互补．
∴∠ABC=∠1；
（2）∵∠ADE=∠B，
∴DE∥BC，
∴∠CED+∠C=180°．
故答案为CD，（两直线平行，内错角相等）；BC，两直线平行，同旁内角互补．
分析：（1）根据两直线平行，内错角相等得到要使∠ABC=∠1，则AB∥CD；
（2）根据同位角相等两直线平行得到DE∥BC，再根据两直线平行，同旁内角互补得到∠CED+∠C=180°．
点评：本题考查了直线平行的判定与性质：同位角相等两直线平行；两直线平行，内错角相等；两直线平行，同旁内角互补．
练习册系列答案
考前必练系列答案
相关题目
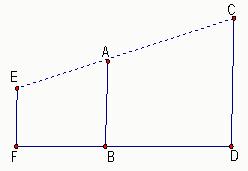
24、如图，在△ABC中，∠ACB=90°，CD⊥AB，垂足为D，点E在CB的延长线上，∠ACD=55°．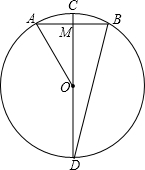
如图，在⊙O中，CD是直径，AB是弦，且CD⊥AB，已知CD=16，AB=8，求证：（1）BD2=DM•CD；
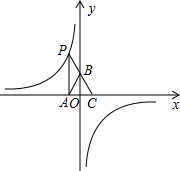（2013•丽水）如图，点P是反比例函数y=
如图，AB∥CD，∠BMN与∠DNM的平分线相交于点G．