题目内容
19. 如图,在等边三角形ABC中,点D,E别在边BC,AC上,BD=CE,AD与BE相交于点P,则△ABD≌△BCE,∠APE=60°.
如图,在等边三角形ABC中,点D,E别在边BC,AC上,BD=CE,AD与BE相交于点P,则△ABD≌△BCE,∠APE=60°.
分析 根据题干条件:AB=BC,BD=CE,∠ABD=∠C可以判定△ABD≌△BCE,即可得到∠BAD=∠CBE,又知∠APE=∠ABP+∠BAP,故知∠APE=∠ABP+∠CBE=∠B.
解答 解:∵△ABC是等边三角形,
∴AB=BC,∠ABC=∠ACB=60°.
在△ABD和△BCE中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABC=∠ACB}\\{BD=CE}\end{array}\right.$,
∴△ABD≌△BCE(SAS),
∴∠BAD=∠DBE.
∵∠APE=∠ABP+∠BAP,
∴∠APE=∠ABP+∠DBE.
即∠APE=∠ABD.
∴∠APE=60°.
故答案为:BCE,60°.
点评 本题主要考查等边三角形的性质和全等三角形的判定与性质的知识点,解答本题的关键是能看出∠APE=∠ABP+∠BAP,还要熟练掌握三角形全等的判定与性质定理.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
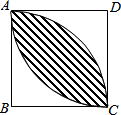 如图所示,若正方形边长为a,则阴影部分的面积为($\frac{1}{2}$π-1)a2.
如图所示,若正方形边长为a,则阴影部分的面积为($\frac{1}{2}$π-1)a2.