题目内容
24、已知AD是△ABC的外角∠EAC的平分线，且AD∥BC，则△ABC的边一定满足
AB=AC或∠B=∠C
．分析：由AD∥BC，根据平行线的性质同位角∠EAD=∠B，内错角∠DAC=∠C，又AD是角平分线，所以∠EAD=∠DAC，所以∠B=∠C，再根据等角对等边的性质也可以得到AB=AC．
解答：
解：∵AD∥BC，
∴∠EAD=∠B，∠DAC=∠C，
∵AD是∠EAC的平分线，
∴∠DAE=∠DAC，
∴∠B=∠C，
∴AB=AC，
即△ABC的边必须满足的条件为AB=AC或∠B=∠C．
故填AB=AC或∠B=∠C．
解：∵AD∥BC，∴∠EAD=∠B，∠DAC=∠C，
∵AD是∠EAC的平分线，
∴∠DAE=∠DAC，
∴∠B=∠C，
∴AB=AC，
即△ABC的边必须满足的条件为AB=AC或∠B=∠C．
故填AB=AC或∠B=∠C．
点评：本题考查了等腰三角形的性质；根据所要的结论推出所需要的条件是本题的求解思路，需要注意，本题要的是边的关系，审题一定要仔细，小心出错．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
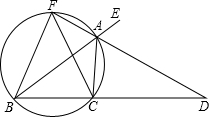于点F，连接FB、FC．
3、如图，已知AD是△ABC的中线，AE=EF=FC，下面给出三个关系式：①AG：AD=1：2；②GE：BE=1：4；③GE：BE=3：4，其中正确的为（ ）
