题目内容
用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点,叫格点,以格点为顶点的多边形叫格点多边形,设格点多边形的面积为S,它各边上格点的个数和为x.
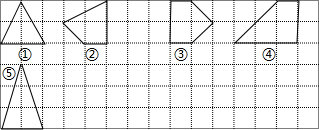
(1)上图中的格点多边形,其内部都只有一个格点,它们的面积与各边上格点的个数和的对应关系如下表:
请写出S与x之间的关系式. 答:S= ;
(2)请你再画出一些格点多边形,使这些多边形内部都有而且只有2格点,如序号⑤.此时所画的各个多边形的面积S与它各边上格点的个数和x之间的关系式是S= ;
(3)请你继续探索,当格点多边形内部有且只有n个格点时,猜想S与x有怎样的关系?

(1)上图中的格点多边形,其内部都只有一个格点,它们的面积与各边上格点的个数和的对应关系如下表:
| 多边形的序号 | ① | ② | ③ | ④ | … |
| 多边形的面积S | 2 | 2.5 | 3 | 4 | … |
| 多边形各边上格点的个数和x | 4 | 5 | 6 | 8 | … |
(2)请你再画出一些格点多边形,使这些多边形内部都有而且只有2格点,如序号⑤.此时所画的各个多边形的面积S与它各边上格点的个数和x之间的关系式是S=
(3)请你继续探索,当格点多边形内部有且只有n个格点时,猜想S与x有怎样的关系?
考点:规律型:图形的变化类
专题:
分析:(1)2=4×
,2.5=5×
,3=6×
,4=8×
多边形的面积=各边上格点个数和的一半,即S=
x;
(2)内部有2个格点就是指图形的中间有2个小正方形的顶点,由此画图;并根据图找出S与x的关系.
(3)由图可知多边形内部都有而且只有n格点时,面积为:S=
x+(n-1).
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)内部有2个格点就是指图形的中间有2个小正方形的顶点,由此画图;并根据图找出S与x的关系.
(3)由图可知多边形内部都有而且只有n格点时,面积为:S=
| 1 |
| 2 |
解答:解:(1)多边形的面积=各边上格点个数和的一半,即S=
x;
(2)如图所示:

根据图可知:
正方形的面积是6,它的各边上格点的个数和x是10,中间格点数是2,
6=10×
+1;
三角形的面积是3,它的各边上格点的个数和x是4,中间格点数是2,
3=4×
+1;
梯形的面积是5,它的各边上格点的个数和x是8,中间格点数是2,
5=8×
+1;
那么S=
x+1;
(3)通过上题探究可知:
最后的1就是内部的格点数2-1而得;
所以格点多边形面积=各边上格点的个数和×
+(多边形内部格点数-1);
即S=
x+(n-1).
| 1 |
| 2 |
(2)如图所示:

根据图可知:
正方形的面积是6,它的各边上格点的个数和x是10,中间格点数是2,
6=10×
| 1 |
| 2 |
三角形的面积是3,它的各边上格点的个数和x是4,中间格点数是2,
3=4×
| 1 |
| 2 |
梯形的面积是5,它的各边上格点的个数和x是8,中间格点数是2,
5=8×
| 1 |
| 2 |
那么S=
| 1 |
| 2 |
(3)通过上题探究可知:
最后的1就是内部的格点数2-1而得;
所以格点多边形面积=各边上格点的个数和×
| 1 |
| 2 |
即S=
| 1 |
| 2 |
点评:此题考查图形的变化规律,需要根据图中表格和自己所算得的数据,总结出规律,利用规律解决问题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
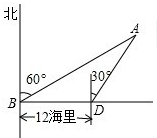 海岛A的周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,在点B处测得海岛A位于北偏东60°,航行12海里后到达点D处,又测得海岛A位于北偏东30°,如果渔船不改变航向继续向东航行.有没有触礁的危险?
海岛A的周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,在点B处测得海岛A位于北偏东60°,航行12海里后到达点D处,又测得海岛A位于北偏东30°,如果渔船不改变航向继续向东航行.有没有触礁的危险?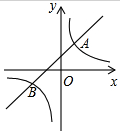 如图,直线y=x+2与双曲线y=
如图,直线y=x+2与双曲线y= 请写出点A,B,C,D,的坐标.
请写出点A,B,C,D,的坐标. 如图,EF∥AD,∠1=∠2.求证:DG∥AB.
如图,EF∥AD,∠1=∠2.求证:DG∥AB. 如图所示,?ABCD中,AM⊥BC于M,AN⊥CD于N,已知AB=10,BM=5,MC=3,则MN的长为
如图所示,?ABCD中,AM⊥BC于M,AN⊥CD于N,已知AB=10,BM=5,MC=3,则MN的长为