题目内容
17．
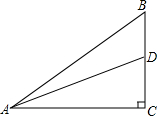如图，在Rt△ABC中，AB=15，Sin∠BAC=$\frac{3}{5}$，点D是BC边上一点，且BD=4，求：（1）线段AC的长；（2）tan∠ADC的值．
分析 （1）根据三角函数的定义可得出BC的长，根据勾股定理得出AC即可；
（2）由BD=4，即可得出CD，再根据正切的定义得出答案即可．
解答 解：（1）∵sin∠BAC=$\frac{3}{5}$，
∴$\frac{BC}{AB}$=$\frac{3}{5}$，
∵AB=15，
∴BC=9，
∵AC2+BC2=AB2，
∴AC=12；
（2）∵BC=9，BD=4，
∴CD=5，
∵tan∠ADC=$\frac{AC}{CD}$，
∴tan∠ADC=$\frac{12}{5}$．
点评 本题考查了解直角三角形，以及勾股定理，熟记三角函数的定义是解题的关键．
练习册系列答案
全优点练单元计划系列答案
相关题目
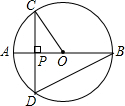已知AB是⊙O的直径，弦CD⊥AB，垂足为P，
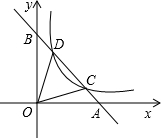如图，直线AB过点A（8，0）、B（0，6）．反比例函数$y=\frac{p}{x}$（p＞0）的图象与直线AB交于C、D两点，连接OC、OD．
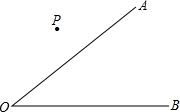读句画图并填空：
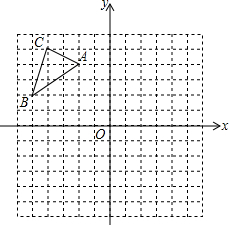已知△ABC在平面直角坐标系中的位置如图所示．将△ABC向右平移6个单位长度，再向下平移4个单位长度得到△A1B1C1．（图中每个小方格边长均为1个单位长度）