题目内容
3.已知函数y=(n+3)x|n|-2是关于x的一次函数,则n=3.分析 因为函数y=(n+3)x|n|-2是关于x的一次函数,可知$\left\{\begin{array}{l}{|n|-2=1}\\{n+3≠0}\end{array}\right.$,求出n即可解决问题.
解答 解:∵函数y=(n+3)x|n|-2是关于x的一次函数,
∴$\left\{\begin{array}{l}{|n|-2=1}\\{n+3≠0}\end{array}\right.$,解得n=3,
故答案为3.
点评 本题考查一次函数的定义,解题的关键是理解一次函数的定义,属于基础题.

练习册系列答案
相关题目

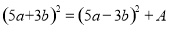 ,则A=( )
,则A=( ) ,则x的值为( )
,则x的值为( ) B.
B.  C.
C.  D.
D. 