题目内容
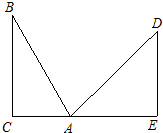 如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点.已知∠BAC=60°,∠DAE=45°,当D到地面的垂直距离DE=2
如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点.已知∠BAC=60°,∠DAE=45°,当D到地面的垂直距离DE=2 m,求点B到地面的垂直距离BC(结果保留根号)
m,求点B到地面的垂直距离BC(结果保留根号)
解:在Rt△DAE中,∵∠DAE=45°,
∴∠ADE=∠DAE=45°,
AE=DE=2 .
.
∴AD2=AE2+DE2=( )2+(
)2+(  )2=16,
)2=16,
∴AD=4,即梯子的总长为4米.
∴AB=AD=4.
在Rt△ABC中,∵∠BAC=60°,
∴∠ABC=30°,
∴AC= AB=2,
AB=2,
∴BC2=AB2-AC2=42-22=12,
∴BC= =
= m,
m,
∴点B到地面的垂直距离BC= m.
m.
分析:在Rt△ADE中,运用勾股定理可求出梯子的总长度,在Rt△ABC中,根据已知条件再次运用勾股定理可求出BC的长.
点评:本题考查了勾股定理的应用,如何从实际问题中整理出直角三角形并正确运用勾股定理是解决此类题目的关键.
∴∠ADE=∠DAE=45°,
AE=DE=2
 .
.∴AD2=AE2+DE2=(
 )2+(
)2+(  )2=16,
)2=16,∴AD=4,即梯子的总长为4米.
∴AB=AD=4.
在Rt△ABC中,∵∠BAC=60°,
∴∠ABC=30°,
∴AC=
 AB=2,
AB=2,∴BC2=AB2-AC2=42-22=12,
∴BC=
 =
= m,
m,∴点B到地面的垂直距离BC=
 m.
m.分析:在Rt△ADE中,运用勾股定理可求出梯子的总长度,在Rt△ABC中,根据已知条件再次运用勾股定理可求出BC的长.
点评:本题考查了勾股定理的应用,如何从实际问题中整理出直角三角形并正确运用勾股定理是解决此类题目的关键.

练习册系列答案
相关题目
 如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点.已知∠BAC=60°,∠DAE=45°,点D到地面的垂直距离DE=3
如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点.已知∠BAC=60°,∠DAE=45°,点D到地面的垂直距离DE=3 如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧的墙上时,梯子的顶端在B点,当它靠在另一侧的墙上时,梯子的顶端在D点,已知∠BAC=60°,∠DAE=45°,点B到地的垂直距离BC=
如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧的墙上时,梯子的顶端在B点,当它靠在另一侧的墙上时,梯子的顶端在D点,已知∠BAC=60°,∠DAE=45°,点B到地的垂直距离BC= 如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点.已知∠BAC=60°,∠DAE=45°,当D到地面的垂直距离DE=2
如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点.已知∠BAC=60°,∠DAE=45°,当D到地面的垂直距离DE=2 如图,在两面墙之间有一根底端在A点的竹竿,当它靠在一侧墙上时,竹竿的顶端在B点;当它靠在另一侧墙上时,竹竿的顶端在D点.已知∠BAC=60°,∠DAE=45°,AC=2米,则DE的高度为
如图,在两面墙之间有一根底端在A点的竹竿,当它靠在一侧墙上时,竹竿的顶端在B点;当它靠在另一侧墙上时,竹竿的顶端在D点.已知∠BAC=60°,∠DAE=45°,AC=2米,则DE的高度为 如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点.已知∠BAC=60°,∠DAE=45°,点D到地面的垂直距离DE=3
如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点.已知∠BAC=60°,∠DAE=45°,点D到地面的垂直距离DE=3