题目内容
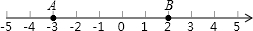数轴上A、B两点所表示的有理数的和是________．
-1
分析：此题借助数轴用数形结合的方法求解．由数轴可知点A表示的数是-3，点B表示的数是2，所以A，B两点所表示的有理数的和是-1．
解答：由数轴得，点A表示的数是-3，点B表示的数是2，
∴A，B两点所表示的有理数的和是-3+2=-1．
点评：本题考查数轴的有关知识．借助数轴来求解，非常直观，且不容易遗漏，体现了数形结合的优点．
分析：此题借助数轴用数形结合的方法求解．由数轴可知点A表示的数是-3，点B表示的数是2，所以A，B两点所表示的有理数的和是-1．
解答：由数轴得，点A表示的数是-3，点B表示的数是2，
∴A，B两点所表示的有理数的和是-3+2=-1．
点评：本题考查数轴的有关知识．借助数轴来求解，非常直观，且不容易遗漏，体现了数形结合的优点．
练习册系列答案
出彩同步大试卷系列答案
相关题目
请把下列每对数在数轴上所对应的两点的距离写在横线上：已知A、B是数轴上的任意两点，分别表示数m、n，且点B在点A的右边，设A、B两点间的距离为d．
（1）填写下表：
| n | 5 | 0 | -3 | -4.5 | 2 |
| m | 3 | -5 | -6 | -6 | -10 |
| d |
（2）请写出d与m、n之间的数量关系式；
（3）已知A、B两点所表示的数分别为-100和100，点P为数轴上的整数点，若点P到A、B两点的距离之和等于200，距离之差大于20，求出符合条件的整数点P的个数以及这些整数的和．
操作与思考
探索性问题：
已知点A，B在数轴上的位置所表示的数分别用
表示．利用数形结合思想回答下列问题：
（1）填写下表：
| 数 | 第1组 | 第2组 | 第3组 | 第4组 | 第5组 | 第6组 | … |
|
| 5 | －5 | 6 | －6 | －10 | －2.5 | … |
|
| 3 | 0 | －4 | －4 | 2 | －2.5 | … |
| A，B两点的距离 | 2 | 0 | … |
（2）通过对上表中具体数据的研究和归纳，你发现数轴上表示
和
两点之间的距离表示为 .
（3）若表示一个有理数，则
的最小值是 .