Question

【题目】如图，在平面直角坐标系中，已知抛物线与轴交于，两点，与轴交于点，连接.

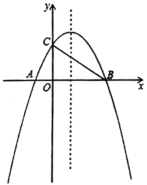
（1）求该抛物线的函数表达式；

（2）若点为抛物线对称轴上一点，抛物线上是否存在点，使得以，，，为顶点的四边形是平行四边形？若存在，请直接写出所有满足条件的点的坐标；若不存在，请说明理由；

（3）点是直线上方抛物线上的点，若，求出点的到轴的距离.

Answer 1

【答案】（1）（2）存在，或或（3）

【解析】

（1）将点A（-1，0），B（3，0）代入y=ax2+bx+2即可；

（2）由题得，，，设，，按照分类讨论的方法得到符合条件的值；

（3）过点作平行于轴交的延长线与点，过点作垂直轴于，先利用平行线的性质、等量代换等求证、，利用勾股定理求出H坐标，写出直线CP的函数表达式，求出一次函数与二次函数的交点P的坐标，即可得到答案.

（1）解：（1）将点，代入，

可得，，

∴；

（2）存在点使得以，，，为顶点的四边形是平行四边形，

由题得，，，设，，

①四边形是平行四边形时，

，∴，

∴；

②四边形时平行四边形时，

，∴，

∴；

③四边形时平行四边形时，

，∴，

∴；

综上所述：或或；

（2）过点作平行于轴交的延长线与点.

∵

∴

又

∴

∴

又

∴

故可设，即

过点作垂直轴于

在中，则

解得

∴

设直线的解析式为

得得，

∴

故

解得（舍去），

即点到轴的距离是