题目内容
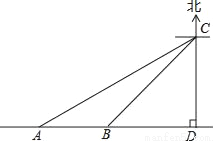
据调查,超速行驶是引发交通事故的主要原因之一.上周末,小明和三位同学用所学过的知识在一条笔直的道路上检测车速.如图,观测点C到公路的距离CD为100米,检测路段的起点A位于点C的南偏西60°方向上,终点B位于点C的南偏西45°方向上.某时段,一辆轿车由西向东匀速行驶,测得此车由A处行驶到B处的时间为4秒.问此车是否超过了该路段16米/秒的限制速度?(参考数据: 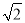 ≈1.4,
≈1.4, 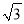 ≈1.7)
≈1.7)
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下表给出了代数式﹣x2+bx+c与x的一些对应值:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
﹣x2+bx+c | … | 5 | n | c | 2 | ﹣3 | ﹣10 | … |
(1)根据表格中的数据,确定b,c,n的值;
(2)设y=﹣x2+bx+c,直接写出0≤x≤2时y的最大值.
(1)b=-2,c=5,n=6;(2)y的最大值是5. 【解析】试题分析:(1)把(﹣2,0)、(1,2)分别代入﹣x2+bx+c中得到关于b、c的方程组,然后解方程组即可得到b、c的值;然后计算x=﹣1时的代数式的值即可得到n的值; (2)利用表中数据即可求解. 试题解析:(1)根据表格数据可得 ,解得, ∴﹣x2+bx+c=﹣x2﹣2x+5, 当x=﹣1时,﹣x2...

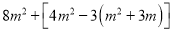 ,其中m=
,其中m=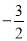
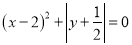 ,求代数式
,求代数式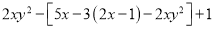 的值
的值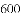
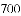
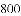
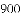
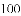
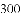
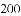
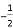 的倒数是( )
的倒数是( ) B. -2 C. 2 D.
B. -2 C. 2 D. 
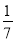 B.
B. 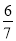 C. ﹣
C. ﹣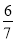 D. 0
D. 0