题目内容
19. 如图,在△ABC中,AB=AC,点D是边BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
如图,在△ABC中,AB=AC,点D是边BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.(1)求证:△ABD≌△ACE;
(2)求证:∠BAC+∠BCE=180°;
(3)当点D在直线BC上移动,则∠BAC与∠BCE之间有怎样的数量关系?请直接写出你的结论.
分析 (1)由已知角相等,利用等式的性质得到夹角相等,利用SAS即可得证;
(2)由(1)的结论,利用全等三角形对应角相等得到∠B=∠ACE,在三角形ABC中,利用内角和定理列出等式,等量代换即可得证;
(3)当点D在射线BC上时;当点D在射线BC的反向延长线上时,找出∠BAC与∠BCE数量关系即可.
解答 (1)证明:∵∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE,
在△ABD和△ACE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$,
∴△ABD≌△ACE(SAS);
(2)证明:∵△ABD≌△ACE,
∴∠B=∠ACE,
在△ABC中,∠BAC+∠B+∠ACB=180°,
∴∠BAC+∠ACE+∠ACB=180°,
∴∠BAC+∠ACE=180°;
(3)解:当点D在射线BC上时,如图1所示,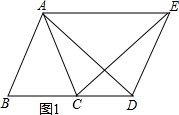
此时∠BAC+∠BCE=180°;
当点D在射线BC的反向延长线上时,如图2所示,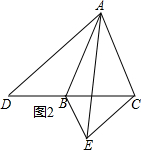
此时∠BAC=∠BCE.
点评 此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
9. 某商场统计了今年1-5月A、B两种品牌冰箱的销售情况,并将获得的数据绘制成如图折线统计图:
某商场统计了今年1-5月A、B两种品牌冰箱的销售情况,并将获得的数据绘制成如图折线统计图:
(1)根据图中数据填写表格.
(2)通过计算该商场这段时间内A、B两种品牌冰箱月销售量的方差,比较这两种品牌冰箱月销售量的稳定性.
 某商场统计了今年1-5月A、B两种品牌冰箱的销售情况,并将获得的数据绘制成如图折线统计图:
某商场统计了今年1-5月A、B两种品牌冰箱的销售情况,并将获得的数据绘制成如图折线统计图:(1)根据图中数据填写表格.
| 1月 | 2月 | 3月 | 4月 | 5月 | 中位数 | 平均数 | |
| A | 15 | 17 | 16 | 13 | 14 | ||
| B | 10 | 14 | 15 | 16 | 15 |
7.用配方法解方程x2-6x+4=0,下列配方正确的是( )
| A. | (x-3)2=13 | B. | (x+3)2=13 | C. | (x-3)2=5 | D. | (x+3)2=5 |
14.过同一平面内不重合的三点中的任意两点可以画出的直线条数是( )
| A. | 1 | B. | 2 | C. | 2或3 | D. | 1或3 |
4.若有理数a与2互为相反数,则a为( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -2 | D. | $-\frac{1}{2}$ |
11.已知:x+y=1,则代数式2x+2y-4的值是( )
| A. | 2 | B. | 6 | C. | -2 | D. | -6 |