题目内容
20. 已知抛物线y=-x2+2x+3.
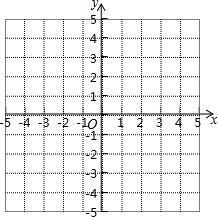
已知抛物线y=-x2+2x+3.(1)用配方法求抛物线的对称轴与顶点坐标,并在如图所示的平面直角坐标系中画出它的图象;
(2)若y>0,根据图象请直接写出x的取值范围.
分析 (1)利用配方法步骤得出二次函数的顶点坐标即可;利用图象与x轴,y轴交点坐标以及顶点坐标,即可得出图象;
(2)利用函数图象,当函数大于0得出,x轴上方部分大于0,即可得出答案.
解答 解:(1)y=-x2+2x+3=-(x2-2x)+3,
=-(x2-2x+1-1)+4,
=-(x-1)2+4,
∴它的顶点坐标为:(1,4);
令y=0
∴0=-(x-1)2+4,
∴x=3或-1,
∴图象与x轴交点坐标为(3,0),(-1,0),对称轴x=(3+(-1))/2=1
令x=0,则y=3,
∴图象与y轴交点坐标为(0,3),如图所示:
(2)由函数的图象可知:当-1<x<3时,y>0.
点评 此题主要考查了二次函数的性质以及配方法求二次函数的顶点坐标,利用数形结合得出图象在x轴上方部分y>0是解题关键.

练习册系列答案
相关题目
11.关于x的一元二次方程x2-mx+2m-1=0的两个实数根分别是x1,x2,且x${\;}_{1}^{2}$+x${\;}_{2}^{2}$=7,则(x1-x2)2的值为( )
| A. | 1 | B. | 12 | C. | 13 | D. | 25 |
8.下列调查中,适合用普查方法的是( )
| A. | 了解一批电视机的使用寿命 | |
| B. | 了解我市居民家庭一周内丢弃塑料袋的数量 | |
| C. | 了解我市中学生的近视率 | |
| D. | 了解我校学生最喜爱的体育项目 |
5.(-0.125)2008×82008+(-1)2008+(-1)2009的值是( )
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
10.下列变形是因式分解的是( )
| A. | x(x+1)=x2+x | B. | x2+2x+1=(x+1)2 | C. | x2+xy-3=x(x+y)-3 | D. | x2+6x+4=(x+3)2-5 |