题目内容
9．在一个正多边形中，一个内角是它相邻的一个外角的3倍．（1）求这个多边形的每一个外角的度数．
（2）求这个多边形的边数．
分析 （1）设这个多边形的每一个外角的度数为x度，根据题意列出方程解答即可；
（2）根据多边形的外角和计算即可．
解答 解：（1）设这个多边形的每一个外角的度数为x度．根据题意，得：
3x+x=180，
解得x=45．
故这个多边形的每一个外角的度数为45°；
（2）360°÷45°=8．
故这个多边形的边数为8．
点评 此题考查多边形的外角和内角，关键是根据多边形的内角和和外角和定理计算．
练习册系列答案
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案
相关题目
17．计算：（-t）6•t2=（ ）
| A． | t8 | B． | -t8 | C． | -t12 | D． | t12 |
4．在一个不透明的袋子中装有红、黄两种颜色的球共20个，每个球除颜色外完全相同．某学习兴趣小组做摸球实验，将球搅匀后从中随机摸出1个球，记下颜色后再放回袋中，不断重复．下表是活动进行中的部分统计数据．
（1）完成上表；
（2）“摸到红球”的概率的估计值是0.6（精确到0.1）
（3）试估算袋子中红球的个数．
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到红球的次数m | 59 | 96 | 118 | 290 | 480 | 601 |
| 摸到红球的频率$\frac{m}{n}$ | 0.59 | 0.64 | 0.58 | 0.58 | 0.60 | 0.601 |
（2）“摸到红球”的概率的估计值是0.6（精确到0.1）
（3）试估算袋子中红球的个数．
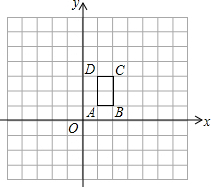已知：如图，长方形ABCD的顶点坐标分别为A（1，1），B（2，1），C（2，3），D（1，3）．
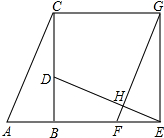如图，已知Rt△ABC中，∠ABC=90°，先把△ABC绕点B顺时针旋转90°至△DBE后，再把△ABC沿射线平移至△FEG，DF、FG相交于点H．
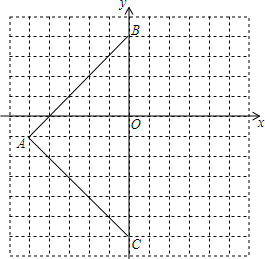如图，三角形ABC在平面直角坐标系中，三个顶点坐标分别为A（-5，-1）、B（0，4）、C（0，-6）．