题目内容
2. 已知,如图?ABCD中,AB⊥AC,AB=1,BC=$\sqrt{5}$,对角线AC、BD交于O点,将直线AC绕点O顺时针旋转,分别交BC、AD于点E、F.
已知,如图?ABCD中,AB⊥AC,AB=1,BC=$\sqrt{5}$,对角线AC、BD交于O点,将直线AC绕点O顺时针旋转,分别交BC、AD于点E、F.(1)连接哪些线段可以构成新的平行四边形?请说明理由;
(2)证明:在旋转过程中,线段AF与EC总保持相等;
(3)在旋转过程中,四边形DEDF可能是菱形吗?如果不能,请说明理由;如果能,说明理并求出此时AC绕点O顺时针旋转的度数.
分析 (1)根据平行四边形的性质得出OA=OC,OB-OD,OE=OF,故可得出结论;
(2)根据ASA定理得出△AOF≌△COE,由此可得出结论;
(3)连接BF,DE,EF与BD互相平分可知,当EF⊥BD时四边形BEDF是菱形,再由勾股定理去除AC的长,根据等腰直角三角形的性质可得出结论.
解答 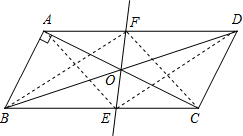 (1)解:连接AE、CF、BF、DE,则可得到?AECF,?BEDF.
(1)解:连接AE、CF、BF、DE,则可得到?AECF,?BEDF.
理由:∵OA=OC,OB=OD,OE=OF,
∴四边形AECF与四边形BEDF是平行四边形;
(2)证明:∵四边形ABCD是平行四边形,
∴$\left\{\begin{array}{l}AO=CO\\∠FAO=∠ECO\\∠AOF=COE\end{array}\right.$,
∴△AOF≌△COE,
∴AF=CE;
(3)解:四边形BEDF可以是菱形.
理由:如图,连接BF,DE,
∵由(2)知△AOF≌△COE,
∴OE=OF,
∴当EF⊥BD时四边形BEDF是菱形.
在Rt△ABC中,
∵AB=1,BC=$\sqrt{5}$,
∴AC=$\sqrt{5-1}$=2,
∴PA=1=AB,
∴∠AOB=45°,
∴∠AOF=90°-45°=45°,
∴AC绕点O顺时针旋转45°时,四边形BEDF是菱形.
点评 本题考查的是几何变换综合题,涉及到平行四边形的判定与性质、全等三角形的判定与性质、菱形的判定与性质等知识,难度适中.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
12.等腰三角形的两边长分别为2cm和7cm,则其周长为( )
| A. | 11cm | B. | 13cm | C. | 16cm | D. | 11cm或16cm |
 如图是正方体的表面展开图,小明事先已把三对相反数填在正方体相对的两个面上.则a=-3,a+b×c=5.
如图是正方体的表面展开图,小明事先已把三对相反数填在正方体相对的两个面上.则a=-3,a+b×c=5.