题目内容
3.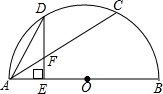 如图,AB为半⊙O的直径,C为弧AB上一点,D为弧AC的中点,DE⊥AB于点E,交AC于点F.求证:
如图,AB为半⊙O的直径,C为弧AB上一点,D为弧AC的中点,DE⊥AB于点E,交AC于点F.求证:(1)DF=AF;
(2)DE=$\frac{1}{2}$AC.
分析 (1)如图,连接BD;首先证明∠DAC=∠ABD;其次证明∠ADE=∠ABD,得到∠ADE=∠DAC,即可解决问题.
(2)如图,连接OD;首先证明AG=GC;其次证明DE=AG,即可解决问题.
解答 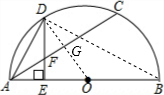 (1)证明:如图,连接BD;OD交AC于点G;
(1)证明:如图,连接BD;OD交AC于点G;
∵D为弧AC的中点,
∴$\widehat{AD}=\widehat{CD}$,∠DAC=∠ABD;
∵AB为半⊙O的直径,且DE⊥AB,
∴∠ADE+∠DAE=∠DAE+∠ABD,
∴∠ADE=∠ABD,
∴∠ADE=∠DAC,
∴DF=AF.
(2)如图,连接OD;
∵D为弧AC的中点,
∴OD⊥AC,AG=GC;
在△ADE与△DAG中,
$\left\{\begin{array}{l}{∠DAG=∠ADE}\\{∠AGD=∠DEA}\\{AD=AD}\end{array}\right.$,
∴△ADE≌△DAG(AAS),
∴DE=AG,
∵AG=$\frac{1}{2}$AC,
∴DE=$\frac{1}{2}$AC.
点评 该题主要考查了垂径定理、圆周角定理及其推论、全等三角形的判定及其性质等几何知识点及其应用问题;解题的关键是作辅助线,灵活运用垂径定理、圆周角定理及其推论等知识点来分析、判断、解答.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
11.如果一组数据5,-2,0,6,4,x的平均数为3,那么x等于( )
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
13.下列式子,一定成立的是( )
| A. | 32=6 | B. | -32=9 | C. | |-23|=8 | D. | (-1)8=-1 |
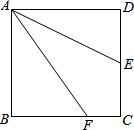 如图,已知正方形ABCD的边长是2厘米,E是CD边的中点,F在BC边上移动,当AE恰好平分∠FAD时,CF=$\frac{1}{2}$厘米.
如图,已知正方形ABCD的边长是2厘米,E是CD边的中点,F在BC边上移动,当AE恰好平分∠FAD时,CF=$\frac{1}{2}$厘米.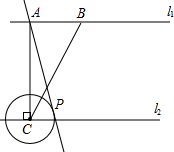 已知,如图l1∥l2,点A、B在直线l1上,AB=3,过点A作AC⊥l2,垂足为点C,AC=4,过点A的直线与直线l2交于点P,以点C为圆心,CP为半径作⊙C.
已知,如图l1∥l2,点A、B在直线l1上,AB=3,过点A作AC⊥l2,垂足为点C,AC=4,过点A的直线与直线l2交于点P,以点C为圆心,CP为半径作⊙C. 如图,已知∠1=100°,∠2=80°,∠3=105°,则∠4=85°.
如图,已知∠1=100°,∠2=80°,∠3=105°,则∠4=85°.