题目内容
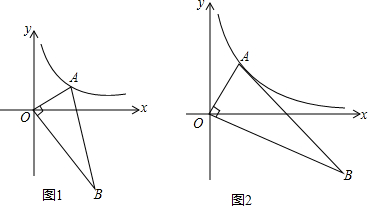
如图,点A是双曲线y=
(x>0)上一个点,连接OA,作OB⊥OA,且AO:BO=1:2.
(1)在双曲线上多次改变A点的位置,得到相应的B点,用平滑的曲线把这些B点连接起来,观察猜想这条曲线的形状,并求B点纵坐标随横坐标变化的函数解析式;
(2)过A点作y轴垂线MA,过B点作x轴垂线BN,MA与BN交于P点,BN交双曲线y=
(x>0)于C点(C点在A点右侧),连接AC,在图2中画出示意图并证明:∠PAC=∠ABO.
| 1 |
| x |
(1)在双曲线上多次改变A点的位置,得到相应的B点,用平滑的曲线把这些B点连接起来,观察猜想这条曲线的形状,并求B点纵坐标随横坐标变化的函数解析式;
(2)过A点作y轴垂线MA,过B点作x轴垂线BN,MA与BN交于P点,BN交双曲线y=
| 1 |
| x |

考点:反比例函数综合题
专题:
分析:(1)设A(a,
),B(x,y),作AC⊥x轴于点C,BD⊥y轴于点D,利用△OCA∽△ODB,即可求出B点纵坐标随横坐标变化的函数解析式;
(2)设A(a,
),B(x,-
),C(x,
),可得出P点坐标为(x,
-
),证出△APC∽△BOA,即可得出∠PAC=∠ABO.
| 1 |
| a |
(2)设A(a,
| 1 |
| a |
| 4 |
| x |
| 1 |
| x |
| 1 |
| a |
| 1 |
| x |
解答:解:(1)如图1,设A(a,
),B(x,y),
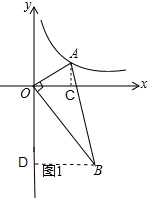
作AC⊥x轴于点C,BD⊥y轴于点D,
∵OB⊥OA,
∴△OCA∽△ODB,
∴
=
,
=
,即
=
,
=
∴
×
=
×
,即y=-
.
(2)如图2,设A(a,
),B(x,-
),C(x,
),
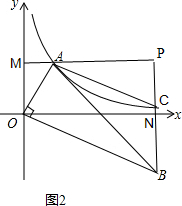
∴P点坐标为(x,
-
)
∵AO:BO=1:2,
=
=
=
,
∴
=
,∠APC=∠BOA,
∴△APC∽△BOA,
∴∠PAC=∠ABO.
| 1 |
| a |

作AC⊥x轴于点C,BD⊥y轴于点D,
∵OB⊥OA,
∴△OCA∽△ODB,
∴
| OC |
| OD |
| OA |
| OB |
| AC |
| BD |
| OA |
| OB |
| a |
| -y |
| 1 |
| 2 |
| ||
| x |
| 1 |
| 2 |
∴
| a |
| -y |
| ||
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| x |
(2)如图2,设A(a,
| 1 |
| a |
| 4 |
| x |
| 1 |
| x |

∴P点坐标为(x,
| 1 |
| a |
| 1 |
| x |
∵AO:BO=1:2,
| PC |
| AP |
| ||||
| x-a |
| 1 |
| ax |
| 1 |
| 2 |
∴
| AO |
| BO |
| PC |
| AP |
∴△APC∽△BOA,
∴∠PAC=∠ABO.
点评:本题主要考查了反比例函数的综合题,解题的关键是利用三角形相似的判定与性质求解.

练习册系列答案
相关题目
下列各式中,正确的是( )
A、
| |||
B、(-
| |||
C、±
| |||
D、
|
在等边△ABC中,已知BC边上的中线AD=16,则∠BAC的平分线长等于( )
| A、4 | B、8 | C、16 | D、32 |
一个三角形的三个内角中至少有( )
| A、一个钝角 |
| B、一个直角 |
| C、一个角大于60° |
| D、两个锐角 |
无论m取何值,下列各式都有意义的是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
