题目内容
若a、b、c是三个非零有理数,则
+
+
的值是( )
| |a| |
| a |
| |b| |
| b |
| |c| |
| c |
分析:根据绝对值的意义得到
=1或-1,
=1或-1,
=1或-1,然后分类讨论:当a、b、c都是正数;当a、b、c只有两个正数;当a、b、c只有一个正数;当a、b、c都是负数.
| |a| |
| a |
| |b| |
| b |
| |c| |
| c |
解答:解:∵a、b、c是三个非零有理数,
∴
=1或-1,
=1或-1,
=1或-1,
当a、b、c都是正数,
+
+
=1+1+1=3;
当a、b、c只有两个正数,
+
+
=1+1-1=1;
当a、b、c只有一个正数,
+
+
=1-1-1=-1;
当a、b、c都是负数,
+
+
=-1-1-1=-3.
故选D.
∴
| |a| |
| a |
| |b| |
| b |
| |c| |
| c |
当a、b、c都是正数,
| |a| |
| a |
| |b| |
| b |
| |c| |
| c |
当a、b、c只有两个正数,
| |a| |
| a |
| |b| |
| b |
| |c| |
| c |
当a、b、c只有一个正数,
| |a| |
| a |
| |b| |
| b |
| |c| |
| c |
当a、b、c都是负数,
| |a| |
| a |
| |b| |
| b |
| |c| |
| c |
故选D.
点评:本题考查了绝对值:若a>0,则|a|=a;若a=0,则|a|=0;若a<0,则|a|=-a.也考查了分类讨论思想的运用.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
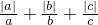 的值是
的值是