Question

已知点P是矩形ABCD边AB上的任意一点（与点A、B不重合）
【小题1】如图①，现将△PBC沿PC翻折得到△PEC；再在AD上取一点F，将△PAF沿PF翻折得到△PGF，并使得射线PE、PG重合，试问FG与CE的位置关系如何，请说明理由；
【小题2】在（1）中，如图②，连接FC，取FC的中点H，连接GH、EH，请你探索线段GH和线段EH的大小关系，并说明你的理由．

Answer 1

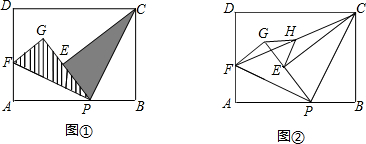
【小题1】FG∥CE．
理由：在矩形ABCD中，∠A=∠B=90°，
由题意得，∠G=∠A=90°，∠PEC=∠B=90°
∴∠GEC=90°，
∴∠G=∠GEC，
∴FG∥CE；
【小题1】GH=EH，
延长GH交CE于点M，如下图所示：
由（1）得，FG∥CE，
∴∠GFH=∠MCH，
∵H为CF的中点，
∴FH=CH，
又∵∠GHF=∠MHC，
∴△GFH≌△MHC，
∴GH=HM=GM，
∵∠GEC=90°，
∴EH=GM，
∴GH=EH．解析:

【小题1】根据矩形的性质以及轴对称的性质可以得到∠G=∠GEC=90°，根据内错角相等，即可证明两条直线平行；
【小题1】延长GH交CE于点M，结合（1）中的结论证明△GFH≌△MHC，再运用直角三角形斜边上的中线等于斜边的一半进行证明结论．