题目内容
3. 如图,已知△ABC内接于⊙O,AB是直径,OD⊥BC于点D.连接DO并延长到F使AF=OC.
如图,已知△ABC内接于⊙O,AB是直径,OD⊥BC于点D.连接DO并延长到F使AF=OC.(1)求证:△AOC≌△OAF;
(2)探究:当∠1等于多少度时,四边形OCAF是菱形?请回答并给予证明.
分析 (1)证出△AOF和△AOC是等边三角形,由SAS即可证出;△AOC≌△OAF;
(2)要四边形OCAF是菱形,需OC=CA=AF=OF,即△AOC为等腰三角形,∠2=60°,那么∠1=30°.
解答 (1)证明:∵AF=OC=OF=AO,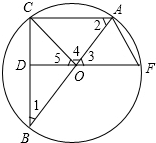
∴△AOF为等边三角形,
∴∠3=60°,且∠3=∠DOB=60°,
又∵OD⊥BC,
∴D是BC的中点,∠1=30°;
∵AB是直径,
∴∠ACB=90°,
∴∠2=60°,
∴△AOC是等边三角形,
∵△AOF是等边三角形,
∴AF=OC=OF=AO,
在△AOC和△OAF中,$\left\{\begin{array}{l}{AC=OF}&{\;}\\{∠2=∠3}&{\;}\\{OA=AO}&{\;}\end{array}\right.$,
∴△AOC≌△AOF(SAS);
(2)解:当∠1=30°时,四边形OCAF是菱形.理由如下:
∵∠1=30°AB是直径,
∴∠BCA=90°,
∴∠2=60°,而OC=OA,
∴△OAC是等边三角形,
∴OA=OC=CA,
又∵D,O分别是BC,BA的中点,
∴DO∥CA,
∴∠2=∠3=60°而OC=OA=AF.
∴△OAF是等边三角形,
∴AF=OA=OF,(9分)
∴OC=CA=AF=OF,
∴四边形OCAF是菱形.
点评 本题考查了全等三角形的判定、等边三角形的判定与性质、菱形的判定、圆周角定理、三角形中位线定理;熟练掌握全等三角形的判定和菱形的判定,证明三角形是等边三角形是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知不等式组$\left\{\begin{array}{l}{2x+3>3x}\\{2x-(x-1)≥-3}\end{array}\right.$,
已知不等式组$\left\{\begin{array}{l}{2x+3>3x}\\{2x-(x-1)≥-3}\end{array}\right.$,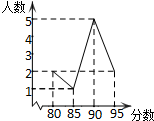 某班10名学生成绩统计如图,则这10名学生成绩中位数是90分,众数是90分.
某班10名学生成绩统计如图,则这10名学生成绩中位数是90分,众数是90分. 要从甲、乙两名同学中选出一名,代表班级参加射击比赛,如图是两人最近10次射击训练成绩的折线统计图.(两同学的射击成绩都取整数环)
要从甲、乙两名同学中选出一名,代表班级参加射击比赛,如图是两人最近10次射击训练成绩的折线统计图.(两同学的射击成绩都取整数环) 如图,把两个大小相同的含30°的角的三角尺如图放置,若AD=4$\sqrt{6}$,试求围成的△ADC的面积.
如图,把两个大小相同的含30°的角的三角尺如图放置,若AD=4$\sqrt{6}$,试求围成的△ADC的面积.