题目内容
如图，⊙O是钝角△ABC的外接圆，连接OC．已知∠BAC=y°，∠BCO=x°，则y与x之间的函数关系式为考点：圆周角定理
专题：
分析：延长CO交⊙O于点D，连接BD，则有∠CBD=90°，由于∠CBD为
度数的一半，∠BCD为
度数的一半，∠BAC为
度数的一半，∠BAC=∠CBD+∠BCD，即y=x+90．
 |
| CD |
|
| BD |
|
| BDC |
解答：
解：延长CO交⊙O于点D，连接BD．
∵CD为⊙O直径，
∴∠CBD=90°，
∵∠CBD为
度数的一半，∠BCD为
度数的一半，∠BAC为
度数的一半，
∴∠BAC=∠CBD+∠BCD，
∴y=x+90．
故答案为y=x+90．
解：延长CO交⊙O于点D，连接BD．∵CD为⊙O直径，
∴∠CBD=90°，
∵∠CBD为
|
| CD |
|
| BD |
|
| BDC |
∴∠BAC=∠CBD+∠BCD，
∴y=x+90．
故答案为y=x+90．
点评：本题考查了圆周角定理，知道圆周角是圆心角的一半即弧的一半是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
在Rt△ABC中，∠ACB=90°，AC=BC=1，将Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE，点B经过的路径为计算-（-2014）的结果是（ ）
| A、-2014 | ||
| B、2014 | ||
C、-
| ||
D、
|
在△ABC中，AB=3，AC=
，BC=
，则tanA=（ ）
| 7 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知点A（2，y1）和点B（m，y2）是抛物线y=x2-2x上两点，且y2＞y1，则m的取值范围是（ ）
| A、m＞2 |
| B、m≤0或m≥2 |
| C、0＜m＜2 |
| D、m＜0或m＞2 |
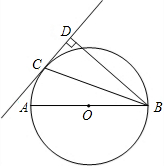如图，点C是以AB为直径的⊙O上的一点，BD与过点C的切线互相垂直，垂足为点D．