题目内容
已知射线OC是∠AOB的平分线,射线OD是∠AOC的三等分线,且∠AOB=72°,求∠COD的度数.
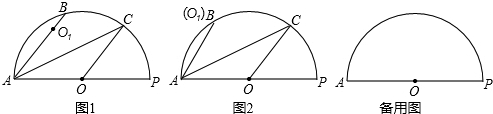
分析:分两种情况考虑:(1)当OD靠近OA时,如图(1)所示,由OC为角平分线,求出∠AOC的度数,根据OD为∠AOC三等分线求出∠AOD度数,即可求出∠COD度数;(2)当OD靠近OC时,如图(2)所示,同理求出∠COD度数.
解答: 解:分两种情况考虑:
解:分两种情况考虑:
(1)当OD靠近OA时,如图(1)所示,
∵OC平分∠AOB,∠AOB=72°,
∴∠AOC=
∠AOB=36°,
∵OD为∠AOC的角平分线,
∴∠AOD=
∠AOC=12°,
则∠COD=∠AOC-∠AOD=24°;
(2)当OD靠近OC时,如图(2)所示,
∵OD为∠AOC的三等分线,
∴∠COD=
∠AOC=12°,
综上,∠COD为24°或12°.
 解:分两种情况考虑:
解:分两种情况考虑:(1)当OD靠近OA时,如图(1)所示,
∵OC平分∠AOB,∠AOB=72°,
∴∠AOC=
| 1 |
| 2 |
∵OD为∠AOC的角平分线,
∴∠AOD=
| 1 |
| 3 |
则∠COD=∠AOC-∠AOD=24°;
(2)当OD靠近OC时,如图(2)所示,
∵OD为∠AOC的三等分线,
∴∠COD=
| 1 |
| 3 |
综上,∠COD为24°或12°.
点评:此题考查了角的计算,以及角平分线定义,利用了分类讨论及数形结合的思想,做出正确的图形是解本题的关键.

练习册系列答案
相关题目

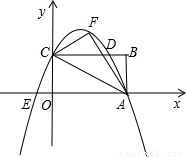
 (2012•枣阳市模拟)已知如图,矩形OABC的长OA=
(2012•枣阳市模拟)已知如图,矩形OABC的长OA=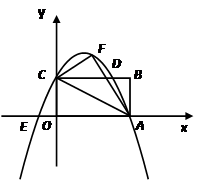
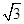 ,宽OC=1,将△AOC沿AC翻折得△AFC.
,宽OC=1,将△AOC沿AC翻折得△AFC. 轴相交于另外一点E,若点M是
轴相交于另外一点E,若点M是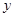 轴上的点,若以点E、M、D、N为顶点的四边形是平行四边形,试求点M、N的坐标
轴上的点,若以点E、M、D、N为顶点的四边形是平行四边形,试求点M、N的坐标 个单位长度的速度从C点出发沿CB 向终点B运动,同时动点Q从A点出发以每秒
个单位长度的速度从C点出发沿CB 向终点B运动,同时动点Q从A点出发以每秒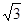 个单位长度的速度沿射线AO运动,当P运动到B点时,P,Q同时停止运动.当点P运动时间t(秒)为何值时,以P、C、O为顶点的三角形与以Q、O、C为顶点的三角形相似?
个单位长度的速度沿射线AO运动,当P运动到B点时,P,Q同时停止运动.当点P运动时间t(秒)为何值时,以P、C、O为顶点的三角形与以Q、O、C为顶点的三角形相似?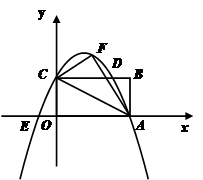
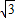 ,宽OC=1,将△AOC沿AC翻折得△AFC.
,宽OC=1,将△AOC沿AC翻折得△AFC.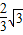 个单位长度的速度从C点出发沿CB 向终点B运动,同时动点Q从A点出发以每秒
个单位长度的速度从C点出发沿CB 向终点B运动,同时动点Q从A点出发以每秒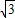 个单位长度的速度沿射线AO运动,当P运动到B点时,P,Q同时停止运动.当点P运动时间t(秒)为何值时,以P、C、O为顶点的三角形与以Q、O、C为顶点的三角形相似?
个单位长度的速度沿射线AO运动,当P运动到B点时,P,Q同时停止运动.当点P运动时间t(秒)为何值时,以P、C、O为顶点的三角形与以Q、O、C为顶点的三角形相似?