题目内容
 (2012•枣阳市模拟)已知如图,矩形OABC的长OA=
(2012•枣阳市模拟)已知如图,矩形OABC的长OA=| 3 |
(1)求过A、F、C三点的抛物线解析式;
(2)设(1)中的抛物线与矩形OABC边CB相交于点D,与x轴相交于另外一点E,若点M是x轴上的点,N是y轴上的点,若以点E、M、D、N为顶点的四边形是平行四边形,试求点M、N的坐标;
(3)若动点P以每秒
| 2 |
| 3 |
| 3 |
| 3 |
分析:(1)根据矩形的边长求得点F的坐标,利用待定系数法求得抛物线的解析式即可;
(2)首先求得抛物线与x轴的交点E的坐标,然后分当DN∥EM且DN=EM时和当M在E点右侧时求得M、N的坐标即可;
(3)若以P、C、Q为顶点的三角形与△QOC相似,因∠POC=∠QCO=90°,则有CQ=OP或OC2=CQ•OP.然后分当P、Q在y轴同侧时和当P、Q在y轴异侧时利用相似三角形的性质列出有关t的方程求解即可.
(2)首先求得抛物线与x轴的交点E的坐标,然后分当DN∥EM且DN=EM时和当M在E点右侧时求得M、N的坐标即可;
(3)若以P、C、Q为顶点的三角形与△QOC相似,因∠POC=∠QCO=90°,则有CQ=OP或OC2=CQ•OP.然后分当P、Q在y轴同侧时和当P、Q在y轴异侧时利用相似三角形的性质列出有关t的方程求解即可.
解答:解: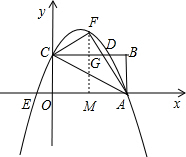 (1)∵OA=
(1)∵OA=
,OC=1,
∴tan∠OAC=
.
∴∠OAC=30°∠ACF=∠ACO=60°…(1分)
过F作FM⊥OA于M,交CB于G,则FG⊥CD.
∠GCF=30°,GF=
CF=
OC=
.
CG=
.
∴F(
,
)…(2分)
设过 A、B、C三点抛物线解析式为y=ax2+bx+c.
∴c=1
∴
…(3分)
解之,得
∴y=-
x2+
x+1.…(4分)
(2)∵由-
x2+
x+1=0,得x1=
,x2=-
.
∴E(-
,0)…(5分)
由-
x2+
x+1=1,得x1=0,x2=
.
∴D(
,1).…(6分)
①当DN∥EM且DN=EM时,当M在E点左侧时,M1(-
,0),此时N1(0,1)…(7分)
当M在E点右侧时,OM2=
.
∴M2(
,0),此时N2(0,1)…(8分)
②当ED∥MN且ED=MN时,过D作DH⊥OA于H,M3(
,0),N3(0,-1)…(9分)
(3)若以P、C、Q为顶点的三角形与△QOC相似,因∠POC=∠QCO=90°,则有
CQ=OP或OC2=CQ•OP.
当P、Q在y轴同侧时:
由
t=
-
t,得t=
.…(10分)
由
t(
-
t)=1,得 2t2-2t+1=0.
△=4-8=-4<0,故无解.
当P、Q在y轴异侧时:
由
t=
t-
,得t=3>
,不合题意,舍去…(11分)
由
t(
t-
)=1,得2t2-2t-1=0.t1=
<0舍去,
t2=
∴t=
或
…(12分)
 (1)∵OA=
(1)∵OA=| 3 |
∴tan∠OAC=
| ||
| 3 |
∴∠OAC=30°∠ACF=∠ACO=60°…(1分)
过F作FM⊥OA于M,交CB于G,则FG⊥CD.
∠GCF=30°,GF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
CG=
| ||
| 2 |
∴F(
| ||
| 2 |
| 3 |
| 2 |
设过 A、B、C三点抛物线解析式为y=ax2+bx+c.
∴c=1
∴
|
解之,得
|
∴y=-
| 4 |
| 3 |
| 3 |
(2)∵由-
| 4 |
| 3 |
| 3 |
| 3 |
| ||
| 4 |
∴E(-
| ||
| 4 |
由-
| 4 |
| 3 |
| 3 |
| 3 |
| 4 |
| 3 |
∴D(
| 3 |
| 4 |
| 3 |
①当DN∥EM且DN=EM时,当M在E点左侧时,M1(-
| 3 |
当M在E点右侧时,OM2=
| ||
| 2 |
∴M2(
| ||
| 2 |
②当ED∥MN且ED=MN时,过D作DH⊥OA于H,M3(
| 3 |
(3)若以P、C、Q为顶点的三角形与△QOC相似,因∠POC=∠QCO=90°,则有
CQ=OP或OC2=CQ•OP.
当P、Q在y轴同侧时:
由
2
| ||
| 3 |
| 3 |
| 3 |
| 3 |
| 5 |
由
2
| ||
| 3 |
| 3 |
| 3 |
△=4-8=-4<0,故无解.
当P、Q在y轴异侧时:
由
2
| ||
| 3 |
| 3 |
| 3 |
| 3 |
| 2 |
由
2
| ||
| 3 |
| 3 |
| 3 |
1-
| ||
| 2 |
t2=
1+
| ||
| 2 |
∴t=
| 3 |
| 5 |
1+
| ||
| 2 |
点评:本题考查了二次函数的综合知识,往往是中考题的压轴题,难度相对比较大.解决此类问题时充分考虑各种情况是解决此类题目的关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 (2012•枣阳市模拟)如图,A,B是⊙O上的两点,∠AOB=120°,C是
(2012•枣阳市模拟)如图,A,B是⊙O上的两点,∠AOB=120°,C是
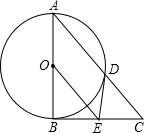 (2012•枣阳市模拟)如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连接DE、OE.
(2012•枣阳市模拟)如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连接DE、OE.