题目内容
 如图是一只鸭子的图案,请探究下列问题:
如图是一只鸭子的图案,请探究下列问题:(1)写出各个顶点的坐标;
(2)试计算图案覆盖的面积.
考点:坐标与图形性质,三角形的面积
专题:数形结合
分析:(1)根据各象限点的坐标特征和坐标轴上点的坐标特征写出各点坐标;
(2)用长为6、宽为3的矩形的面积分别减去三个三角形的面积和一个梯形的面积进行计算.
(2)用长为6、宽为3的矩形的面积分别减去三个三角形的面积和一个梯形的面积进行计算.
解答:解:(1)A(-1,0),B(0,1),C(1,1),D(1,-1),E(5,1),F(4,-2);
(2)图案覆盖的面积=6×3-
•1•1-
•(1+2)•2-
•1•3-
•2•4=9.
(2)图案覆盖的面积=6×3-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了坐标与图形性质:利用点的坐标计算相应的线段的长和判断线段与坐标轴的位置关系.解决本题的关键是根据所给条件得到三角形相应的底边和高的长度.

练习册系列答案
相关题目
2015个同学站成一排报数,报出奇数的退出,偶数的留下;留下的同学位置不动重新报数,报到奇数的退出,偶数的留下…如此继续,最后留下一个同学,则最后留下的这个同学第一次站的位置是第( )
| A、256个 | B、512个 |
| C、1024个 | D、2013个 |
 如图,在△ABC中,AB=7cm,AC=4cm,AD为中线,则△ABD与△ACD的周长之差=
如图,在△ABC中,AB=7cm,AC=4cm,AD为中线,则△ABD与△ACD的周长之差=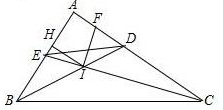 如图,△ABC中,∠A=90°,角平分线BD、CE交于点I,IF⊥CE交CA于F,IH⊥AB于H,下列结论:①∠DIF=45°;②CF+BE=BC;③AE+AF=2AH;④S四边形BEDC=2S△IBC,其中正确的结论为
如图,△ABC中,∠A=90°,角平分线BD、CE交于点I,IF⊥CE交CA于F,IH⊥AB于H,下列结论:①∠DIF=45°;②CF+BE=BC;③AE+AF=2AH;④S四边形BEDC=2S△IBC,其中正确的结论为 如图,△ABC中,∠BAC=90°,∠ABC=∠ACB,∠BDC=∠BCD,∠1=∠2,求∠3的度数.
如图,△ABC中,∠BAC=90°,∠ABC=∠ACB,∠BDC=∠BCD,∠1=∠2,求∠3的度数.