题目内容
1.(1)如图①,O是等边△ABC内一点,OA=6,OB=8,OC=10,将线段BO绕点B逆时针旋转60°得到线段BO',连结线段OO',AO',试判断△AOO'的形状.(2)点D是以AB为斜边的等腰直角三角形ABC内一点,且BD=1,CD=2,AD=3.
(Ⅰ)求∠BDC的度数;
(Ⅱ)求△ABC的面积.
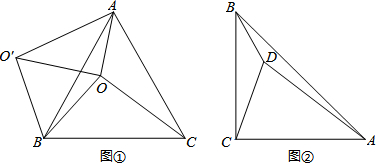
分析 (1)利用旋转的性质得BO=BO′,∠OBO′=60°,则△OBO′为等边三角形,所以OO′=OB=8,则可判断△ABC为等边三角形,所以∠ABC=60°,BA=BC,接着利用旋转的定义可把△BOC绕点B逆时针旋转60°得到△BO′A,于是得到AO′=CO=10,然后根据勾股定理的逆定理可判断△AOO'为直角三角形,∠AOO′=90°;
(2)(Ⅰ)将△CBD绕点B顺时针旋转90°得到△CAD′,如图②,根据旋转的性质得∠DCD′=90°,∠CD′A=∠CDB,CD′=CD=2,AD′=BD=1,则可判断△CDD′为等腰直角三角形,所以∠CD′D=45°,DD′=$\sqrt{2}$CD=2$\sqrt{2}$,然后根据勾股定理的逆定理可判断△ADD'为直角三角形,∠AD′D=90°;则∠AD′C=135°,所以∠BDC=135°;
(Ⅱ)利用△CDD′为等腰直角三角形得到∠CDD′=45°,再判断点B、D、D′共线得到△BD′A为直角三角形,然后利用△ABC的面积=S△CDD′+S△BD′A进行计算.
解答 解:(1)∵线段BO绕点B逆时针旋转60°得到线段BO',
∴BO=BO′,∠OBO′=60°,
∴△OBO′为等边三角形,
∴OO′=OB=8,
∵△ABC为等边三角形,
∴∠ABC=60°,BA=BC,
∴△BOC绕点B逆时针旋转60°得到△BO′A,
∴AO′=CO=10,
在△AOO′中,∵AO′=10,AO=6,OO′=8,
而62+82=102,
∴OA2+OO′2=AO′2,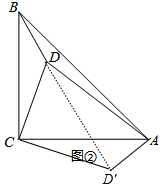
∴△AOO'为直角三角形,∠AOO′=90°;
(2)(Ⅰ)将△CBD绕点B顺时针旋转90°得到△CAD′,如图②,
∴∠DCD′=90°,∠CD′A=∠CDB,CD′=CD=2,AD′=BD=1,
∴△CDD′为等腰直角三角形,
∴∠CD′D=45°,DD′=$\sqrt{2}$CD=2$\sqrt{2}$,
在△ADD′中,AD=3,AD′=1,DD′=2$\sqrt{2}$,
而12+(2$\sqrt{2}$)2=32,
∴D′A2+AD2=DD′2,
∴△ADD'为直角三角形,∠AD′D=90°;
∴∠AD′C=135°,
∴∠BDC=135°;
(Ⅱ)∵△CDD′为等腰直角三角形,
∴∠CDD′=45°,
而∠BDC=135°;
∴∠CDD′+∠BDC=180°,
∴点B、D、D′共线,
∴△BD′A为直角三角形,
∴△ABC的面积=S△CDD′+S△BD′A
=$\frac{1}{2}$×2×2+$\frac{1}{2}$×1×(1+2$\sqrt{2}$)
=$\frac{5}{2}$+$\sqrt{2}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等边三角形的判定与性质和等腰直角直角三角形的判定与性质.

| 的士类型 | 起步价 | 超出起步里程后的收费 | 燃油附加费 |
| 红色的士 | 10元/2千米 | 2.4元/千米 | 3元/每次 |
| 绿色的士 | 6元/1.5千米 | 2.4元/千米 | 2元/每次 |
(2)若小丽乘坐红色的士去博物馆,共付了车费37元,则她乘车走了多少千米?
(3)若小丽身上仅有56元,她乘坐绿色的士最远能走多少千米?
 如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数.
如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数.